题目内容
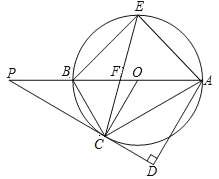
【题目】如图所示,AB 是⊙O 的直径,P 为 AB 延长线上的一点,PC 切⊙O 于点 C,AD⊥PC, 垂足为 D,弦 CE 平分∠ACB,交 AB 于点 F,连接 AE.
(1)求证:PC=PF;
(2)若 tan∠ABC=![]() ,AE=5
,AE=5![]() ,求线段 PC 的长.
,求线段 PC 的长.
【答案】(1)见解析;(2)PC=12.
【解析】(1)由切线得:OC⊥PC,再得平行,由同圆的半径相等:OA=OC,根据等边对等角可得结论;
(2)证明∠PFC=∠PCF,根据等角对等边可得结论;
(3)根据三角函数的比设未知数,利用勾股定理列方程可得结论.
(1)证明:∵PC 为⊙O 的切线,
∴OC⊥PC,
∵AD⊥PC,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠OAC,
∴AC 平分∠DAB;
∵CE 平分∠ACB,
∴∠ACE=∠BCE,
∴![]() ,
,
∴∠ABE=∠ECB,
∵∠BCP+∠OCB=∠BCP+∠OBC=∠BAC+∠OBC=90°,
∴∠BCP=∠BAC,
∵∠BAC=∠BEC,
∴∠BCP=∠BEC,
∵∠PFC=∠BEC+∠ABE,∠PCF=∠ECB+∠BCP,
∴∠PFC=∠PCF,
∴PC=PF;
(2)∵![]() ,
,
∴AE=BE=5![]() ,
,
又∵AB 是直径,
∴∠AEB=90°,
AB=![]() BE=10,
BE=10,
∴OB=OC=5,
∵∠PCB=∠PAC,∠P=∠P,
∴△PCB∽△PAC,
∴![]() ,
,
∵tan∠ABC=![]() ,
,
∴![]() .
.
设 PB=2x,则 PC=3x,
在 Rt△POC 中,(2x+5)2=(3x)2+52, 解得 x1=0(舍)x2=4,
∵x>0,
∴x=4,
∴PC=3x=3×4=12.

练习册系列答案
相关题目