Question

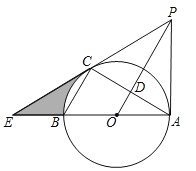
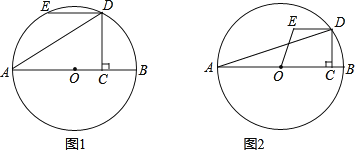
【题目】如图，AB是⊙O的直径，C为半径OB上一点，过点C作CD⊥AB，交上半圆于D，连接AD，将线段CD绕D点顺时针旋转90°到ED．

（1）如图1，当点E在⊙O上时，求证：CD＝2OC；

（2）如图2，当tanA＝时，连接OE，求sin∠EOC的值．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）如图1，作辅助线，构建四边形CDEF，证明四边形CDEF是正方形，得EF＝CD＝CF，再根据HL证明Rt△OFE≌△Rt△OCD，可得结论；

（2）如图2，作辅助线，根据三角函数可设CD＝3a，则AC＝9a，设OA＝OD＝r，则OC＝9a﹣r，在Rt△OCD中用勾股定理可求得，r＝5a，最后根据三角函数的定义可得结论．

（1）证明：如图1，过点E作EF⊥AB于F，连接OD、OE，

由旋转得：∠CDE＝90°，CD＝DE，

∵∠EFC＝∠OCD＝90°，

∴四边形CDEF是正方形，

∴EF＝CD＝CF，

在Rt△OFE和Rt△OCD中，

∵

∴Rt△OFE≌△Rt△OCD（HL），

∴OF＝OC＝CF＝CD

∴CD＝2OC；

（2）解：如图2，过点E作EF⊥AB于F，连接OD，

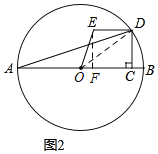
由tan∠BAD＝，

可设CD＝3a，则AC＝9a，设OA＝OD＝r，则OC＝9a﹣r，

在Rt△OCD中，由勾股定理得：OD2＝OC2+CD2，即r2＝（9a﹣r）2+（3a）2，

解得：r＝5a，

即OA＝OD＝5a，OC＝4a，EF＝CF＝3a，OF＝a，

∴OE=，

∴sin∠EOC＝．