题目内容
【题目】如图,在边长为2的正方形ABCD中,E,F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确都有( )个.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四边形ECFG=2S△BGE
;④S四边形ECFG=2S△BGE
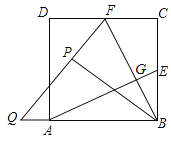
A.5B.4C.3D.2
【答案】C
【解析】
①△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB;
②首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可得到AE⊥BF;
③利用等面积法求得BG的长度;
④利用QF=QB,解出BP,QB,根据正弦的定义即可求解;
⑤根据AA可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解.
解:①根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,故正确;
②∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在△ABE和△BCF中,
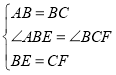 ,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF,故正确;
③由②知,△ABE≌△BCF,则AE=BF=![]() ,
,
∵AE⊥BF
∴![]() ABBE=
ABBE=![]() AEBG,故BG=
AEBG,故BG=![]() .
.
故错误;
④由①知,QF=QB,
令PF=k(k>0),则PB=2k
在Rt△BPQ中,设QB=x,
∴x2=(x﹣k)2+4k2,
∴x=![]() ,
,
∴sin∠BQP=![]() ,故正确;
,故正确;
⑤∵∠BGE=∠BCF,∠GBE=∠CBF,
∴△BGE∽△BCF,
∵BE=![]() BC,BF=
BC,BF=![]() BC,
BC,
∴BE:BF=1:![]() ,
,
∴△BGE的面积:△BCF的面积=1:5,
∴S四边形ECFG=4S△BGE,故错误.
综上所述,共有3个结论正确.
故选C.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案