Question

【题目】如图，在△ABC中，AB=AC，D是BC边上一点，连接AD，E为△ABC外一点，连接DE，AE和BE，AD=DE，BE∥AC.求证：∠BED=∠DAB.

Answer 1

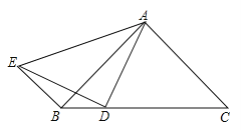
【答案】见解析

【解析】

证明两角相等，可以通过证明全等三角形得到对应角相等，从而证明两角相等.此时要构造出全等三角形，构造全等三角形时，注意把已知的两组边相等AD=DE和两组所求的角相等∠BED=∠DAB，分别构造在同一个一个三角形中，一般作垂线构造直角三角形.构造出来直角三角形后，证明直角三角形可以用HL定理.此时只需要用角平分线的性质证明两个小直角边DM=DN即可.

证明：如图，作DN⊥AB，DM⊥BE，垂足分别为N，M，

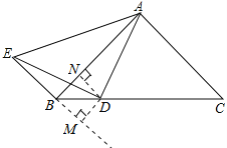
∵AB=AC，

∴∠ABC=∠C

∵BE∥AC，

∴∠C=∠DBM

∴∠NBD=∠MBD即BD平分∠ABM

∵DN⊥AB，DM⊥BE

∴DM=DN(角平分线上的点到角两边的距离相等)

在△AND和△EMD中

∴Rt△AND≌Rt△EMD(HL)，

∠DAB=∠BED