题目内容
【题目】定义:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的三分线,在△ABC中,∠B=30°,AD和 DE是△ABC的三分线,点D在 BC 边上,点E在 AC边上,且AD=BD,DE=CE,请写出∠C所有可能的度数________.
【答案】20°或 40°
【解析】
用量角器,直尺标准作 30°角,而后确定一边为 BA,一边为 BC,根据题意可以先固定 BA 的长,而后可确定 D 点,再标准作图实验﹣﹣分别考虑 AD 为等腰三角形的腰或者底边,兼顾 A、E、C 在同一直线上,易得 2 种三角形 ABC.根据图形易得 x 的值.
解:设∠C=x°.
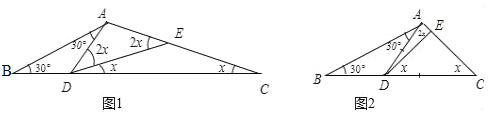
①当 AD=AE 时,
∵2x+x=30+30,
∴x=20.
②当 AD=DE 时,
∵30+30+2x+x=180,
∴x=40.
所以∠C 的度数是 20°或 40°.
故答案 20°或 40°.

练习册系列答案
相关题目