题目内容
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点O与坐标原点重合,顶点A、C在坐标轴上,
的顶点O与坐标原点重合,顶点A、C在坐标轴上,![]() ,将矩形沿
,将矩形沿![]() 折叠,使点A与点C重合.
折叠,使点A与点C重合.

(1)求点E的坐标;
(2)点P从O出发,沿折线![]() 方向以每秒2个单位的速度匀速运动,到达终点E时停止运动,设P的运动时间为t,
方向以每秒2个单位的速度匀速运动,到达终点E时停止运动,设P的运动时间为t,![]() 的面积为S,求S与t的关系式,直接写出t的取值范围;
的面积为S,求S与t的关系式,直接写出t的取值范围;
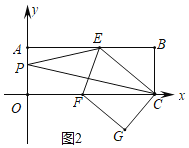
(3)在(2)的条件下,当![]() 时,在平面直角坐标系中是否存在点Q,使得以点P、E、G、Q为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q的坐标.
时,在平面直角坐标系中是否存在点Q,使得以点P、E、G、Q为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q的坐标.
【答案】(1)E(10,6);(2)S= -8t+54(0≤t≤3)或S=-6t+48(3<t≤8);(3)存在, Q(14.4,-4.8)或(18.4,-4.8).
【解析】
(1)设AE=x,根据勾股定理列方程得:(18-x)2+62=x2,解出可得结论;
(2)分两种情况:P在OA或AE上,分别根据三角形面积列式即可;
(3)先根据![]() 分别计算PA和PE的长,如图4,过G作GH⊥OC于H,设OF=y,根据勾股定理列方程可得y的值,利用面积法计算GH的长,得G的坐标,根据平行四边形的性质和平移规律可得Q的坐标.
分别计算PA和PE的长,如图4,过G作GH⊥OC于H,设OF=y,根据勾股定理列方程可得y的值,利用面积法计算GH的长,得G的坐标,根据平行四边形的性质和平移规律可得Q的坐标.
解:(1)如图1,矩形ABCO中,B(18,6),
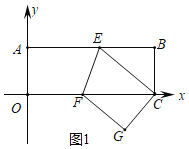
∴AB=18,BC=6,
设AE=x,则EC=x,BE=18-x,
Rt△EBC中,由勾股定理得:EB2+BC2=EC2,
∴(18-x)2+62=x2,
x=10,
即AE=10,
∴E(10,6);
(2)分两种情况:
①当P在OA上时,0≤t≤3,如图2,
S=S矩形OABC-S△PAE-S△BEC-S△OPC,
=18×6-![]() ×10(6-2t)-
×10(6-2t)-![]() ×8×6-
×8×6-![]() ×18×2t,
×18×2t,
=-8t+54,
②当P在AE上时,3<t≤8,如图3,
S=![]() PEBC=
PEBC=![]() ×6×(162t)=3(16-2t)=-6t+48;
×6×(162t)=3(16-2t)=-6t+48;
(3)存在,由PA=![]() PE可知:P在AE上,如图4,过G作GH⊥OC于H,
PE可知:P在AE上,如图4,过G作GH⊥OC于H,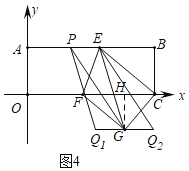
∵AP+PE=10,
∴AP=6,PE=4,
设OF=y,则FG=y,FC=18-y,
由折叠得:∠CGF=∠AOF=90°,
由勾股定理得:FC2=FG2+CG2,
∴(18-y)2=y2+62,
y=8,
∴FG=8,FC=18-8=10,![]() FCGH=
FCGH=![]() FGCG,
FGCG,![]() ×10×GH=
×10×GH=![]() ×6×8,
×6×8,
GH=4.8,
由勾股定理得:FH=![]() =6.4,
=6.4,
∴OH=8+6.4=14.4,
∴G(14.4,-4.8),
∵点P、E、G、Q为顶点的四边形为平行四边形,且PE=4,
∴Q(14.4,-4.8)或(18.4,-4.8).

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案