题目内容
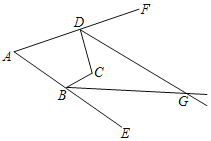
【题目】如图,四边形ABCD的两个外角∠CBE,∠CDF的平分线交于点G,若∠A=52°,∠DGB=28°,则∠DCB的度数是( )
A. 152°B. 128°C. 108°D. 80°
【答案】C
【解析】
连接AC,BD,由三角形外角定义可得∠FDC=∠DAC+∠DCA,∠CBE=∠BAC+∠BCA,再由DG平分∠FDC,BG平分∠CBE,可得∠CBG+∠CDG=![]() (∠DAB+∠DCB),在△BDG中,根据三角形内角和定理可得∠G+∠CDG+∠CBG+∠CDB+∠DBC=180°,将式子进行等量代换即可求解.
(∠DAB+∠DCB),在△BDG中,根据三角形内角和定理可得∠G+∠CDG+∠CBG+∠CDB+∠DBC=180°,将式子进行等量代换即可求解.
连接AC,BD,

∴∠FDC=∠DAC+∠DCA,∠CBE=∠BAC+∠BCA,
∵DG平分∠FDC,BG平分∠CBE,
∴∠CBG+∠CDG=![]() (∠DAB+∠DCB),
(∠DAB+∠DCB),
在△BDG中,∠G+∠CDG+∠CBG+∠CDB+∠DBC=180°,
∴∠G+![]() (∠DAB+∠DCB)+∠CDB+∠DBC=180°,
(∠DAB+∠DCB)+∠CDB+∠DBC=180°,
∴∠G+![]() (∠DAB+∠DCB)+(180°-∠DCB)=180°,
(∠DAB+∠DCB)+(180°-∠DCB)=180°,
∵∠A=52°,∠DGB=28°,
∴28°+![]() ×52°+
×52°+![]() ×∠DCB+180°-∠DCB=180°,
×∠DCB+180°-∠DCB=180°,
∴∠DCB=108°;
故选:C.

练习册系列答案
相关题目






