题目内容
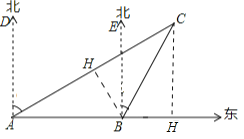
【题目】如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.

(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航行方向不变,当渔船继续航行多长时间时,才能与小岛C的距离最短.
【答案】(1)20![]() 海里;(2)当渔船继续航行20分钟才能与小岛C的距离最短.
海里;(2)当渔船继续航行20分钟才能与小岛C的距离最短.
【解析】
(1)作BH⊥AC于H.首先证明AB=BC,AH=HC,求出HC即可解决问题;
(2)作CH⊥AB交AB的延长线于H.求出BH即可解决问题;
(1)作BH⊥AC于H.
∵∠CBD=∠CAB+∠BCA,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠BAC=30°
∴BA=BC=30×![]() =20海里.
=20海里.
∵BH⊥AC,
∴AH=HC=ABcos30°=10![]() 海里,
海里,
∴AC=2AH=20![]() 海里.
海里.
(2)作CH⊥AB交AB的延长线于H.
在Rt△BCH中,BH=BCcos60°=10海里,
∴时间t=![]() 小时=20分钟.
小时=20分钟.
∴当渔船继续航行20分钟才能与小岛C的距离最短.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



