��Ŀ����
����Ŀ�����⣺̽��������ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ�����ͼ�������ʽ�����̽����������С����̽�����̣��벹��������
�ں���![]() �У��Ա���
�У��Ա���![]() ����������ʵ����
����������ʵ����
��1���±���![]() ��
��![]() �ļ����Ӧֵ��
�ļ����Ӧֵ��
| �� | -3 | -2 | -1 | 0 | 1 | 2 | 3 | �� |
| �� | 1 | 0 | -1 | -2 | -1 | 0 |
| �� |
��![]() ______��
______��
����![]() ��
��![]() Ϊ�ú���ͼ���ϲ�ͬ�����㣬��
Ϊ�ú���ͼ���ϲ�ͬ�����㣬��![]() ______��
______��
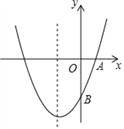
��2����ͼ����ƽ��ֱ������ϵ![]() �У�������ϱ��и��Զ�ӦֵΪ����ĵ㣮����������ĵ㣬�����ú�����ͼ��
�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣮����������ĵ㣬�����ú�����ͼ��
��3�����ݺ���ͼ��ɵú��������ʣ�
�ٸú�������СֵΪ______��
����д���ú���һ������____________��
���𰸡���1����1����-10����2����ͼ����������3����-2���ڵ�x��0ʱ��y��x�����������x��0ʱ��y��x���������С��
��������
��1���ٰ�x=3����y=|x|-2���������m��
�ڰ�y=8����y=|x|-2���������n��
��2��������㷨�����ú�����ͼ����⣻
��3���ٸ��ݺ���ͼ����⼴�ɣ�
�ڸ���ͼ��ɵ������ԣ�
�⣺��1���ٰ�x=3����y=|x|-2����m=3-2=1��
�ʴ�Ϊ1��
�ڰ�y=8����y=|x|-2����8=|x|-2��
���x=-10��10��
��A��n��8����B��10��8��Ϊ�ú���ͼ���ϲ�ͬ�����㣬
��n=-10��
�ʴ�Ϊ-10��
��2���ú�����ͼ����ͼ��ʾ��
��3������ͼ���֪���ú�������СֵΪ-2��
�ʴ�Ϊ-2��
�ڵ�x��0ʱ��y��x�����������
��x��0ʱ��y��x���������С��
�ʴ�Ϊ����x��0ʱ��y��x�����������x��0ʱ��y��x���������С��
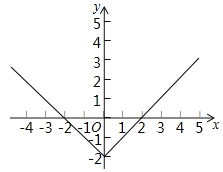

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�