Question

如图1，在正方形ABCD中，等腰三角形AEF的顶点E，F分别在BC和CD上.
（1）求证：BE=DF；
（2）若等腰三角形AEF的腰AE比正方形ABCD的边AB长1，BE=5，求正方形ABCD的面积；
（3）若∠EAF=50°，则
①如图1，∠BAE=         °；

②如图2，将△AEF绕顶点A旋转，在旋转过程中，当BE=DF时，求∠BAE的大小．

Answer 1

（1）根据正方形及等腰三角形的性质即可根据“HL”证得结论；（2）144；
（3）①；②160°

试题分析：（1）根据正方形及等腰三角形的性质即可根据“HL”证得结论；
（2）设，则，在中，根据勾股定理即可列方程求出x，再根据正方形的面积公式即可求得结果；
（3）①先根据“SAS”证得△ABE≌△ADE，再根据正方形的性质即可求得结果；
②先根据“SSS”证得△ABE≌△ADF，即可得到∠BAE=∠DAF，从而可得∠BAF=∠DAE，再根据∠EAF与∠BAD的度数结合周角为360°即可求得结果.
（1），

，
．
，

，
；
（2）设， 则，
在中，，
，
即，
解得，
，
；
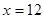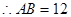（3）①；
②，

，
，
，
即．
，
，
．
点评：解答本题的关键是熟练掌握判定两个三角形全等的一般方法：SSS、SAS、ASA、AAS、HL，注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．