题目内容
在四边形ABCD中，对角线相交于点O；E、F、G、H分别是AD、BD、BC、AC的中点．
（1）说明四边形EFGH是平行四边形；
（2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并说明理由.
（1）说明四边形EFGH是平行四边形；
（2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并说明理由.
（1）∵E、F分别是AD，BD的中点，G、H分别中BC，AC的中点，∴EF∥AB，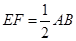
，GH ∥AB，
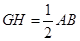，∴EF∥GH，
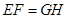，∴四边形EFGH是平行四边形
（2）当
时，四边形EFGH是菱形
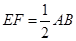，GH ∥AB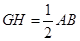，，∴EF∥GH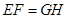，，∴四边形EFGH是平行四边形（2）当
时，四边形EFGH是菱形试题分析：（1）通过G、H分别为BC、AC中点，可以推出EF∥AB，进而求出EF∥GH
（2）∵E、F分别是AD，BD的中点，G、F分别是BC，AC的中点，∴
，
，∵，∴
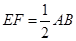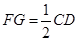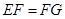，∴平行四边形EFGH是菱形点评：本题考查的是平行四边形和菱形的判定，两者关键都在于要证明有两组边平行且对应相等，而菱形还要注意的是各边都相等
练习册系列答案
阅读快车系列答案
相关题目
______cm.
