题目内容
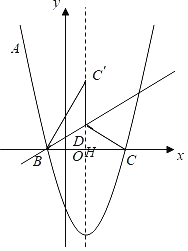
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;

【答案】(1)y=x2﹣2x﹣3;(2)点C′的坐标为(1,2![]() ),点D的坐标为(1,
),点D的坐标为(1,![]() )
)
【解析】
(1)根据抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,利用待定系数法求得该抛物线的解析式即可;
两点,利用待定系数法求得该抛物线的解析式即可;
(2)先确定二次函数对称轴,BC长度,根据题意和翻折的性质,得到B C′长度,利用三角函数求出∠C′BC,再根据角平分线求出∠DBC,解直角三角形可以求得点![]() 和点
和点![]() 的坐标,本题得以解决.
的坐标,本题得以解决.
解:(1)∵抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点,
∴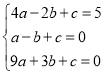 ,得
,得 ,
,
即抛物线的函数表达式是y=x2﹣2x﹣3;
(2)∵与x轴相交于B(﹣1,0),C(3,0)两点,
∴BC=3﹣(﹣1)=3+1=4,该抛物线的对称轴是直线x=![]() =1,
=1,
设抛物线的对称轴与x轴的交点为H,
则点H的坐标为(1,0),
∴BH=2,
∵将△BCD沿直线BD翻折得到△BC′D,点C′恰好落在抛物线的对称轴上,
∴BC=BC′=4,∠C′HB=90°,∠C′BD=∠DBC,
∴OC′=![]() =2
=2![]() ,cos∠C′BH=
,cos∠C′BH=![]() =
=![]() =
=![]() ,
,
∴C′的坐标为(1,2![]() ),∠C′BH=60°,
),∠C′BH=60°,
∴∠DBC=30°,
∵BH=2,∠DBH=30°,
∴OD=BHtan30°=2×![]() =
=![]() ,
,
∴点D的坐标为(1,![]() ),
),
由上可得,点C′的坐标为(1,2![]() ),点D的坐标为(1,
),点D的坐标为(1,![]() ).
).

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:

b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.