题目内容
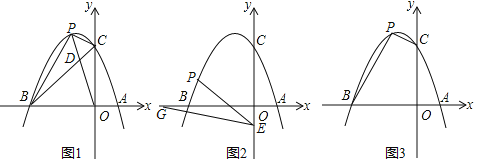
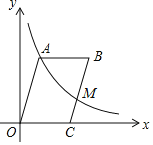
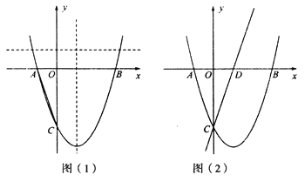
【题目】如图(1),已知抛物线![]() 与x轴交于A、B两点,与y轴负方向交于C点,且
与x轴交于A、B两点,与y轴负方向交于C点,且![]() .
.
(1)试求出抛物线的解析式;
(2)E为直线![]() 上.动点,F为抛物线对称轴上一点,当F点在对称轴上何处时,四边形ACFE的周长最短,并求出此时四边形的周长;
上.动点,F为抛物线对称轴上一点,当F点在对称轴上何处时,四边形ACFE的周长最短,并求出此时四边形的周长;
(3)如图(2),![]() 为x轴上一点,抛物线上x轴的上方是否存在点P,使得线段AP与直线CD相交且它们的夹角为45°,若存在这样的P点,请求出P点坐标;若不存在,请说明理由.
为x轴上一点,抛物线上x轴的上方是否存在点P,使得线段AP与直线CD相交且它们的夹角为45°,若存在这样的P点,请求出P点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)四边形ACFE的最短周长
;(2)四边形ACFE的最短周长![]() ,
,![]() ;(3)存在这样的P点,且
;(3)存在这样的P点,且![]()
【解析】
(1)令y=0,可求得A(-1.0),B(3,0),根据条件求出点C的坐标,把点C的坐标代入抛物线的解析式求出a即可;
(2)设点A关于直线y=1的对称点![]() ,点C关于抛物线对称轴的对称点
,点C关于抛物线对称轴的对称点![]() ,连接
,连接![]() 与直线y=1交于点E,与对称轴交于点F,此时四边形ACEF的周长最短,求出直线
与直线y=1交于点E,与对称轴交于点F,此时四边形ACEF的周长最短,求出直线![]() 与对称轴的交点即可;
与对称轴的交点即可;
(3)设AP交CD于M,连BC.可证![]() ,得出
,得出![]() ,过M作
,过M作![]() 轴于E,则可证
轴于E,则可证![]() ,得到
,得到![]() ,
,![]() ,得到AM的解析式
,得到AM的解析式![]() ,联立方程组即可求解.
,联立方程组即可求解.
解:(1)![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .∴
.∴![]() ,∴
,∴![]()
(2)设A关于![]() 的对称点为
的对称点为![]() ,则
,则![]() ,设C关于抛物线对称轴
,设C关于抛物线对称轴![]() 的对称点为
的对称点为![]() 则
则![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
则有![]() ,解得
,解得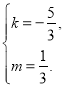
∴![]() ,当
,当![]() 时,
时,![]() ,∴
,∴![]() .
.
四边形ACFE的最短周长![]() ,
,
![]() ,
,![]() .
.
∴四边形ACFE的最短周长![]() ,此时
,此时![]() .
.
(3)设AP交CD于M,连BC.
可证:![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() .
.
过M作![]() 轴于E,则可证
轴于E,则可证![]() ,
,
∴![]() ,即
,即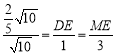 .
.
∴![]() ,
,![]() ,
,
∴AM的解析式为:![]() .
.
由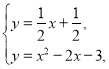 解得
解得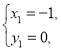 舍去
舍去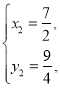
∴存在这样的P点,且![]()

练习册系列答案
相关题目