Question

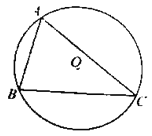
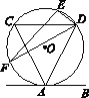
【题目】如图，直线AB与⊙O相切于点A，弦CD∥AB，E、F为圆上的两点，且∠CDE＝∠ADF.若⊙O的半径为，CD＝4，则弦EF的长为( )

A. 4 B. 2

C. 5 D. 6

Answer 1

【答案】B

【解析】

首先连接OA，并反向延长交CD于点H，连接OC，由直线AB与⊙O相切于点A，弦CD∥AB，可求得OH的长，然后由勾股定理求得AC的长，又由∠CDE=∠ADF，可证得EF=AC，继而求得答案．

详解;连接OA，并反向延长交CD于点H，连接OC，

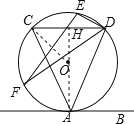
∵直线AB与⊙O相切于点A，

∴OA⊥AB，

∵弦CD∥AB，

∴AH⊥CD，

∴CH=CD=×4=2，

∵⊙O的半径为，

∴OA=OC=，

∴OH==，

∴AH=OA+OH=+=4，

∴AC==2.

∵∠CDE=∠ADF，

∴，

∴，

∴EF=AC=2.

故选：B.