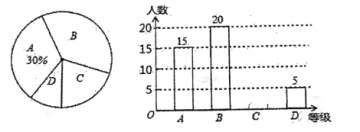
题目内容
【题目】已知△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,若![]() ,如图①.
,如图①.
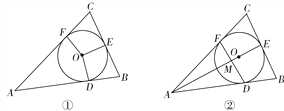
(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图②,AF=2FC=4,求AM的长.
【答案】(1)等腰三角形 (2)![]()
【解析】(1)、易证∠EOF+∠C=180°,∠DOE+∠B=180°和∠EOF=∠DOE,即可解题;(2)、连接OB、OC、OD、OF,易证AD=AF,BD=CF可得DF∥BC,再根据AE长度即可解题.
(1)等腰三角形.
证明:∵AC,AB,BC是⊙O的切线, ∴∠BDO=∠BEO=∠CFO=∠CEO=90°.
∵![]() =
=![]() ,∴∠EOF=∠EOD, ∴∠B=∠C,∴AB=AC, 即△ABC是等腰三角形;
,∴∠EOF=∠EOD, ∴∠B=∠C,∴AB=AC, 即△ABC是等腰三角形;
(2)∵AC=AB,CE=BE, ∴AE⊥BC,∠FAO=∠DAO,∵AF=AD,
∴FM=DM,AE⊥DF,∴AE过圆心O,DF∥BC,∴AF∶AC=DF∶BC,即4∶6=DF∶4,
∴DF=![]() ,∴FM=
,∴FM=![]() , ∴AM=
, ∴AM=![]() =
=![]() .
.

练习册系列答案
相关题目