题目内容
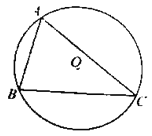
【题目】已知在△ABC中，∠ABC和∠ACB的角平分线交于O，且∠ABC的角平分线与∠ACB的外角平分线交于P，∠OPC和∠OCP角平分线交于H，∠H=117.5°，则∠A=________
【答案】70°
【解析】
根据三角形内角和定理，可得∠HCP+∠HPC=62.5°，由角平分线的性质，得∠OCP+∠OPC=125°，由三角形外角性质，得到∠BOC的度数，然后∠OBC+OCB=55°，然后可以计算得到∠A的度数.
解：∵∠H=117.5°，
∴∠HCP+∠HPC=180°-117.5°=62.5°，
∵CH平分∠OCP，PH平分∠OPC，
∴∠OCP+∠OPC=2（∠HCP+∠HPC）= 125°，
∴∠BOC=125°，
∴∠OBC+∠OCB=180°-125°=55°，
∵BO平分∠ABC，CO平分∠ACB，
∴∠ABC+∠ACB=2（∠OBC+OCB）=110°，
∴∠A=180°-110°=70°；
故答案为：70°.
练习册系列答案
相关题目
