题目内容
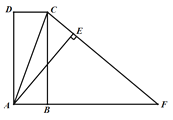
【题目】如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E.
(1)求证:AD=AE.
(2)连结CA,若∠DCA=70°,求∠CAE的度数.

【答案】(1)证明见解析;(2)20°
【解析】证明:(1)∵CF=AF,∴∠FCA=∠CAF
∵四边形ABCD是矩形 , ∴ DC∥AB ∴ ∠DCA=∠CAF ,
∴∠FCA=∠DCA
∵AE⊥FC ∴∠CEA=90°∴∠CDA=∠CEA=90°,
又∵CA=CA,∴△ADC≌△CAE ∴AD=AE
(方法不限,也可以先证△CBF≌△ABE)
(2)∵△ADC≌△CAE ∴∠CAE=∠CAD
∵四边形ABCD是矩形 ,∴∠D=90°
∴∠CAD=![]()
∴∠CAE=20°

练习册系列答案
相关题目