题目内容
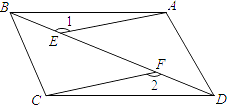
【题目】(1)正方形ABCD与等腰直角三角形PAQ如图1所示重叠在一起,其中∠PAQ=90°,点Q在BC上,连接PD,△ADP与△ABQ全等吗?请说明理由.
(2)如图2,O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N,使探索OM与ON的数量关系,并说明理由.
(3)如图3,将(2)中的“正方形”改成“长方形”,其它的条件不变,且AB=4,AD=6,FM=x,FN=y,试求y与x之间的函数关系式.
【答案】(1)△ADP≌△ABQ,理由见解析;
(2)AC⊥BD,理由见解析;
(3)y与x之间的函数关系式为: ![]() .
.
【解析】试题分析:(1)根据正方形的性质和等腰直角三角形的性质就可以求得△ADP与△ABQ全等;
(2)根据正方形的性质和等腰直角三角形的性质就可以得△ANO≌△BMO,从而得出ON=OM;
(3)过点O作OE⊥AB于E,OH⊥BC于H,由条件求出OE、OH的值,再通过证明△OEN∽△OHM,利用相似三角形的性质就可以求出结论.
试题解析:(1)△ADP≌△ABQ.
理由:如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADP=∠BAD=90°
∵△PAQ是等腰直角三角形,
∴AQ=AP.
∵∠PAQ=90°,
∴∠BAD=∠PAQ,
∴∠BAD-∠QAD=∠PAQ-∠QAD,
∴∠BAQ=∠PAD.
∵在△ADP和△ABQ中,
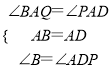
∴△ADP≌△ABQ(ASA);
(2)OM=ON.
理由:如图2,∵四边形ABCD是正方形,
∴AO=BO,∠AOB=90°,∠OAB=∠OBC=45°.
∴∠AOB=∠POQ,
∴∠AOB-∠NOB=∠POQ-∠NOB,
∴∠AON=∠BOM
∵在△AON和△BOM中,
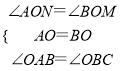 ,
,
∴△AON≌△BOM(ASA)
∴OM=ON;
(3)如图4,
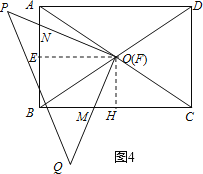
过点O作OE⊥AB于E,OH⊥BC于H,
∴∠OEN=∠OHM=90°,OE=![]() AD,OH=
AD,OH=![]() AB.
AB.
∵AB=4,AD=6,
∴OE=3,OH=2.
∵∠ABC=90°,
∴四边形EBHO是矩形,
∴∠EOH=90°,
∴∠EOH=∠POQ,
∴∠EOH-∠EOM=∠POQ-∠EOM,
∴∠EON=∠HOM.
∴△OEN∽△OHM,
∴![]() ,
,
即![]()
∴y= ![]() .
.