��Ŀ����
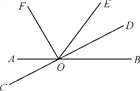
����Ŀ����ͼ1��E��ֱ��AB��CD�ڲ�һ�㣬AB��CD������EA��ED��
��1��̽�����룺������A=30������D=40�������AED���ڶ��ٶȣ�
������A=20������D=60�������AED���ڶ��ٶȣ�
�۲���ͼ1�С�AED����EAB����EDC�Ĺ�ϵ��֤����Ľ��ۣ�
��2����չӦ�ã���ͼ2���߶�FE�볤����ABCD�ı�AB���ڵ�E�����CD ���ڵ�F��ͼ2�Т٢ڷֱ��DZ��߶�FE������2���������߽磩��P��λ���������������ڵ�һ�㣬�����PEB����PFC����EPF�Ĺ�ϵ����Ҫ��˵�����ɣ���
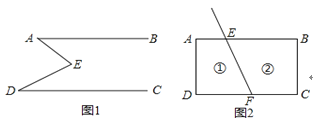
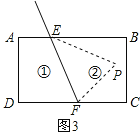
���𰸡���1����70�㣻��80�㣻�ۡ�AED=��EAB+��EDC����2��p���������ʱ����PEB+��PFC+��EPF=360�� ��p���������ʱ����EPF=��PEB+��PFC
�������������������1���ٸ���ͼ�β���ó�����Ƕ������ɣ�
�ڸ���ͼ�β���ó�����Ƕ������ɣ�
�۲���õ����ǹ�ϵ������Ϊ���ӳ�AE��DC����F�㣬��AB��DCƽ�У�������ֱ��ƽ���ڴ�����ȵõ�һ�Խ���ȣ�������������ʼ������������ɵ�֤��
��2������������ֱ��ҳ������ǹ�ϵ���ɣ�
�����������1���ٵ���A=30������D=40�������AED=70��
�ڵ���A=20������D=60�������AED=80��
�ۡ�AED����EAB����EDC�Ĺ�ϵΪ��AED=��EAB+��EDC
֤����ͼ1����E��EF//AB, ���AEF=��A.
��AB//CD, ��EF//CD. ���FED=��D.
���AED=��AEF+��FED=��A+��D.
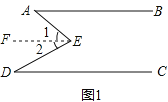
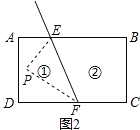
��2��ͼ2��p���������ʱ����PEB+��PFC+��EPF=360��
ͼ3��p���������ʱ����EPF=��PEB+��PFC

 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�