题目内容
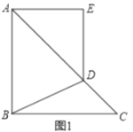
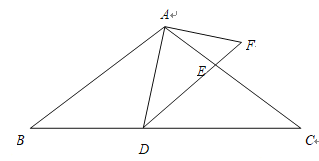
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点(点
边上的一个动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合).以
重合).以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 平分
平分![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)当
;(3)当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长11或
的长11或![]() 或
或![]()
【解析】
(1)根据题意证明![]() 即可求解;
即可求解;
(2)根据![]() 平分
平分![]() 得到
得到![]() ,再根据
,再根据![]() 得到
得到![]() 得到
得到![]() ,从而得到
,从而得到![]() ,即可求解;
,即可求解;
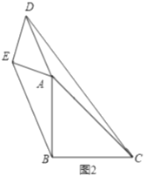
(3)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,根据三线合一得到
,根据三线合一得到![]() ,由勾股定理得出
,由勾股定理得出![]() ,再得到
,再得到![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,根据
,根据![]() 得到
得到![]() ,再分①点
,再分①点![]() 在线段
在线段![]() 的延长线上, ②点
的延长线上, ②点![]() 在线段
在线段![]() 上,当
上,当![]() 是等腰三角形进行讨论求解.
是等腰三角形进行讨论求解.
(1)证明:![]()
![]()
即![]()
![]()
![]()
![]()
![]()
![]()
(2)![]()
![]() 平分
平分![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
又![]() 是公共角,
是公共角,![]()
![]()
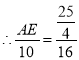
![]()
(3)过点![]() 作
作![]() ,垂足为
,垂足为![]()
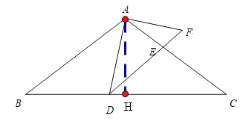
![]()
![]()
由勾股定理得出![]() ,
,![]()
![]()
![]()
设![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]()
①点![]() 在线段
在线段![]() 的延长线上,当
的延长线上,当![]() 是等腰三角形时,存在以下三种情况:
是等腰三角形时,存在以下三种情况:
1.![]() ,则
,则![]()
![]()
2.![]() ,则
,则![]()
![]()
3.![]() ,则
,则![]()
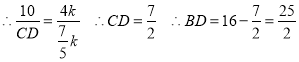
②点![]() 在线段
在线段![]() 上,当
上,当![]() 是等腰三角形时,
是等腰三角形时,
![]()
![]()
![]() 是一个钝角
是一个钝角
![]() 只存在
只存在![]() 这种可能,则
这种可能,则![]()
![]()
![]() ,不符合题意,舍去
,不符合题意,舍去
综上所述,当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长11或
的长11或![]() 或
或![]() .
.

练习册系列答案
相关题目