Question

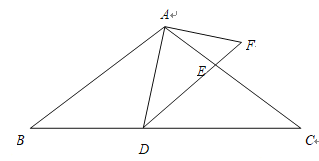
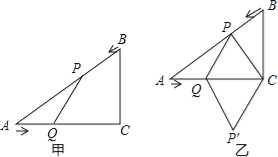
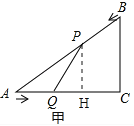
【题目】如图甲，在△ABC中，∠ACB=90°，AC=4cm，BC=3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连接PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：

（1）设△APQ的面积为S，当t为何值时，S取得最大值？S的最大值是多少？

（2）如图乙，连接PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；′

（3）当t为何值时，△APQ是等腰三角形？

Answer 1

【答案】(1)当t为秒时，S最大值为cm2;

当四边形PQP′C为菱形时，t的值是s；

当t为s或s或s时，△APQ是等腰三角形．

【解析】

试题

（1）过点P作PH⊥AC于H，由△APH∽△ABC，得出=，从而求出AB，再根据=，得出PH=3﹣t，则△AQP的面积为：AQPH=t（3﹣t），最后进行整理即可得出答案；

（2）连接PP′交QC于E，当四边形PQP′C为菱形时，得出△APE∽△ABC，=，求出AE=﹣t+4，再根据QE=AE﹣AQ，QE=QC得出﹣t+4=﹣t+2，再求t即可；

（3）由（1）知，PD=﹣t+3，与（2）同理得：QD=﹣t+4，从而求出PQ=，/span>

在△APQ中，分三种情况讨论：①当AQ=AP，即t=5﹣t，②当PQ=AQ，即=t，③当PQ=AP，即=5﹣t，再分别计算即可

试题解析：

解：（1）如图甲，过点P作PH⊥AC于H，

∵∠C=90°，

∴AC⊥BC，

∴PH∥BC，

∴△APH∽△ABC，

∴=，

∵AC=4cm，BC=3cm，

∴AB=5cm，

∴=，

∴PH=3﹣t，

∴△AQP的面积为：

S=×AQ×PH=×t×（3﹣t）=﹣（t﹣）2+，

∴当t为秒时，S最大值为cm2．

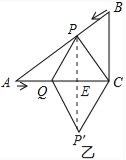
（2）如图乙，连接PP′，PP′交QC于E，

当四边形PQP′C为菱形时，PE垂直平分QC，即PE⊥AC，QE=EC，

∴△APE∽△ABC，

∴=，

∴AE===﹣t+4

QE=AE﹣AQ═﹣t+4﹣t=﹣t+4，

QE=QC=（4﹣t）=﹣t+2，

∴﹣t+4=﹣t+2，

解得：t=，

∵0＜＜4，

∴当四边形PQP′C为菱形时，t的值是s；

（3）由（1）知，

PD=﹣t+3，与（2）同理得：QD=AD﹣AQ=﹣t+4

∴PQ===，

在△APQ中，

①当AQ=AP，即t=5﹣t时，解得：t1=；

②当PQ=AQ，即=t时，解得：t2=，t3=5；

③当PQ=AP，即=5﹣t时，解得：t4=0，t5=；

∵0＜t＜4，

∴t3=5，t4=0不合题意，舍去，

∴当t为s或s或s时，△APQ是等腰三角形．