题目内容
【题目】如图所示,AB∥CD,试解决下列问题:
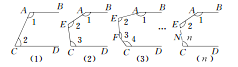
(1)在图(1)中,∠1+∠2等于多少度?请说明理由;
(2)在图(2)中∠1+∠2+∠3等于多少度?请说明理由;
(3)在图(n)中,试探究∠1+∠2+∠3+∠4+…+∠n等于多少度.
【答案】(1) ∠1+∠2=180°, 理由见解析; (2)∠1+∠2+∠3=360°,理由见解析; (3)∠1+∠2+∠3+∠4+…+∠n=180°(n- 1).
【解析】试题分析: (1)根据平行线的性质推出即可;
(2)根据同旁内角互补,两直线平行推出即可;
(3)根据(1)(2)的结果得出即可.
试题解析:
(1)因为AB∥CD,
所以∠1+∠2=180°(两直线平行,同旁内角互补).
(2)如图(1)所示,过点E作EF平行于AB,
因为AB∥CD,AB∥EF,
所以CD∥EF,
所以∠1+∠AEF=180°,∠FEC+∠3=180°,
所以∠1+∠2+∠3=360°.
(3)如图(2)所示,过点E,F分别作EG,FH平行于AB,
因为AB∥CD,
所以AB∥EG∥FH∥CD,
所以∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°,
所以∠1+∠2+∠3+∠4=540°.
如图(4)所示,根据上述规律,显然作(n- 2)条辅助线,运用(n- 1)次两条直线平行,同旁内角互补,即可得到∠1+∠2+∠3+∠4+…+∠n=180°(n- 1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目