题目内容
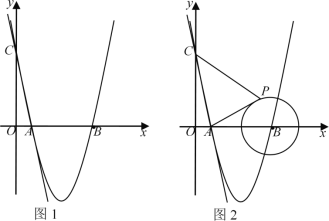
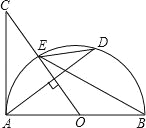
【题目】已知点A是双曲线y=-![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,点C在第一象限,且∠ACB=120°,点C的位置随着点A的运动在不断变化,但始终在双曲k线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,点C在第一象限,且∠ACB=120°,点C的位置随着点A的运动在不断变化,但始终在双曲k线y=![]() 上,则k的值为_______.
上,则k的值为_______.
【答案】1
【解析】
要求k的值,就是要求xy的值,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,则只要求出OECE的值即可.
连接OC,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,如图所示,
∵等腰△ABC中,∠ACB=120°,
∴CO⊥AB,∠CAB=30°,
∴∠AOD+∠COE=90°,
∵∠DAO+∠AOD=90°,
∴∠DAO=∠COE,
∵∠ADO=∠CEO=90°,
∴△AOD∽△OCE,
∴![]() 60°=
60°=![]() ,
,
则![]() ,
,
∵点A是双曲线y=-![]() 在第二象限分支上的一个动点,
在第二象限分支上的一个动点,
∴S△AOD=![]() ,
,
∴S△OCE=![]() ,
,
∴ECEO=1,
∴k=1.
故答案为:1.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目