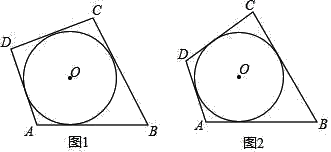题目内容
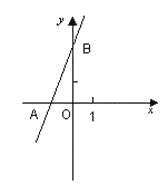
【题目】已知抛物线与x轴的交点坐标分别为A（1，0），B（x2，0）（点B在点A的右侧），其对称轴是x=3，该函数有最小值是﹣2．
（1）求二次函数解析式；
（2）在图1上作平行于x轴的直线，交抛物线于C（x3，y3），D（x4，y4），求x3+x4的值；
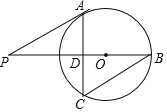
（3）将（1）中函数的部分图象（x＞x2）向下翻折与原图象未翻折的部分组成图象“G”，如图2，在（2）中平行于x轴的直线取点E（x5，y5）、（x4＜x5），结合函数图象求x3+x4+x5的取值范围．
【答案】(1) y=
（x﹣3）2﹣2．（2）x3+x4=6．（3）11＜x3+x4+x5＜9+2
．
【解析】
（1）利用二次函数解析式的顶点式求得结果即可；
（2）根据二次函数图象的对称性质解答；
（3）由已知条件可知直线与图象“G”要有3个交点．
分类讨论：分别求得平行于x轴的直线与图象“G”有2个交点、1个交点时x3+x4+x5的取值范围，易得直线与图象“G”要有3个交点时x3+x4+x5的取值范围．
（1）由上述信息可知该函数图象的顶点坐标为：（3，﹣2），设二次函数的表达式为：y=a（x﹣3）2﹣2．
∵该函数图象经过点A（1，0），∴0=a（x﹣3）2﹣2，解得：a=，∴二次函数解析式为：y=（x﹣3）2﹣2．
（2）由二次函数图象的对称性质得出当纵坐标相等时，x3+x4=6．
（3）由已知条件可知直线与图象“G”要有3个交点．
①当直线与x轴重合时，有2个交点，由二次函数图象的轴对称性质可求x3+x4+x5＞11．
②当直线经过y=（x﹣3）2﹣2的图象顶点时，有2个交点，由翻折可以得到翻折后函数图象为y=﹣（x﹣3）2+2．
令﹣（x﹣3）2+2=﹣2时，解得：x=3±2，其中x=3﹣2（舍去），∴x3+x4+x5＜9+2．
综上所述：11＜x3+x4+x5＜9+2．
