题目内容
【题目】如图，在△ABC中，CA=CB，∠ACB=90°，AB=4，点D为AB的中点，以点D为圆心作圆，半圆恰好经过三角形的直角顶点C，以点D为顶点，作90°的∠EDF，与半圆交于点E，F，则图中阴影部分的面积是____．
【答案】π﹣2．
【解析】
连接CD，作DM⊥BC，DN⊥AC，证明△DMG≌△DNH，则S四边形DGCH=S四边形DMCN，求得扇形FDE的面积，则阴影部分的面积即可求得．
连接CD，作DM⊥BC，DN⊥AC．
∵CA=CB，∠ACB=90°，点D为AB的中点，∴DC=
AB=2，四边形DMCN是正方形，DM=
．
则扇形FDE的面积是：
=π．
∵CA=CB，∠ACB=90°，点D为AB的中点，∴CD平分∠BCA．
又∵DM⊥BC，DN⊥AC，∴DM=DN．
∵∠GDH=∠MDN=90°，∴∠GDM=∠HDN．在△DMG和△DNH中，∵
，∴△DMG≌△DNH（AAS），∴S四边形DGCH=S四边形DMCN=2．
则阴影部分的面积是：π﹣2．
故答案为：π﹣2．
【题目】如图，A、B、C是三个垃圾存放点，点B、C分别位于点A的正北和正东方向，AC=200米，编号为1﹣6号的6名同学分别测得∠C的度数如下表：
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | |
∠C（单位：度） | 37 | 36 | 37 | 40 | 34 | 38 |
他们又调查了各点的垃圾量，并绘制了下列尚不完整的统计图，如图：
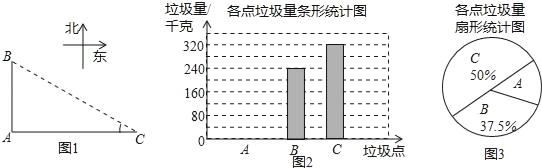
（1）求表中∠C度数的平均数，众数和中位数；
（2）求A处的垃圾量，并将图2补充完整；
（3）用（1）中的
作为∠C的度数，要将A处的垃圾沿道路AB都运到B处，已知运送1千克垃圾每米的费用为0.005元，求运垃圾所需的费用：（注：sin37°=0.6，cos37°=0.8，tan37°=0.75）
【题目】为了争创全国文明卫生城市，优化城市环境，某市公交公司决定购买一批共10台全新的混合动力公交车，现有A、B两种型号，其中每台的价格，年省油量如下表：
A | B | |
价格（万元/台） | a | b |
节省的油量（万升/年） | 2.4 | 2 |
经调查，购买一台A型车比购买一台B型车多20万元，购买2台A型车比购买3台B型车少60万元．
（1）请求出a和b；
（2）若购买这批混合动力公交车（两种车型都要有）每年能节省的汽油量不低于22.4万升，请问有哪几种购车方案？
（3）求（2）中最省钱的购买方案所需的购车款．
