题目内容
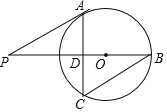
【题目】如图，已知⊙O的半径为5，PA是⊙O的一条切线，切点为A，连接PO并延长，交⊙O于点B，过点A作AC⊥PB交⊙O于点C、交PB于点D，连接BC，当∠P=30°时，
（1）求弦AC的长；
（2）求证：BC∥PA．
【答案】（1）5
；（2）证明见解析.
【解析】试题分析：（1）连接OA，由于PA是⊙O的切线，从而可求出∠AOD=60°，由垂径定理可知：AD=DC，由锐角三角函数即可求出AC的长度．
（2）由于∠AOP=60°，所以∠BOA=120°，从而由圆周角定理即可求出∠BCA=60°，从而可证明BC∥PA
试题解析：（1）连接OA，∵PA是⊙O的切线，∴∠PAO=90°．
∵∠P=30°，∴∠AOD=60°，∵AC⊥PB，PB过圆心O，∴AD=DC．
在Rt△ODA中，AD=OAsin60°=
，∴AC=2AD=
；
（2）∵AC⊥PB，∠P=30°，∴∠PAC=60°，∵∠AOP=60°，∴∠BOA=120°，∴∠BCA=60°，∴∠PAC=∠BCA，∴BC∥PA．
练习册系列答案
相关题目
【题目】如图，A、B、C是三个垃圾存放点，点B、C分别位于点A的正北和正东方向，AC=200米，编号为1﹣6号的6名同学分别测得∠C的度数如下表：
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | |
∠C（单位：度） | 37 | 36 | 37 | 40 | 34 | 38 |
他们又调查了各点的垃圾量，并绘制了下列尚不完整的统计图，如图：
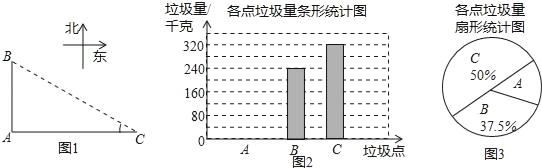
（1）求表中∠C度数的平均数，众数和中位数；
（2）求A处的垃圾量，并将图2补充完整；
（3）用（1）中的
作为∠C的度数，要将A处的垃圾沿道路AB都运到B处，已知运送1千克垃圾每米的费用为0.005元，求运垃圾所需的费用：（注：sin37°=0.6，cos37°=0.8，tan37°=0.75）
