题目内容
【题目】(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形
(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系
猜想结论: (要求用文字语言叙述)
写出证明过程(利用图1,写出已知、求证、证明)
(性质应用)
①初中学过的下列四边形中哪些是圆外切四边形 (填序号)
A:平行四边形:B:菱形:C:矩形;D:正方形
②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是 .
③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.
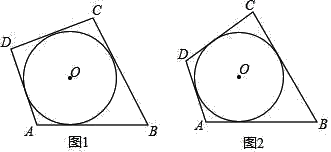
【答案】见解析.
【解析】
(1)根据切线长定理即可得出结论;
(2)①圆外切四边形是内心到四边的距离相等,即可得出结论;
②根据圆外切四边形的对边和相等,即可求出结论;
③根据圆外切四边形的性质求出第四边,利用周长建立方程求解即可得出结论.
性质探讨:圆外切四边形的对边和相等,理由:
如图1,已知:四边形ABCD的四边AB,BC,CD,DA都于⊙O相切于G,F,E,H.
求证:AD+BC=AB+CD.
证明:∵AB,AD和⊙O相切,∴AG=AH,同理:BG=BF,CE=CF,DE=DH,∴AD+BC=AH+DH+BF+CF=AG+BG+CE+DE=AB+CD,即:圆外切四边形的对边和相等.
故答案为:圆外切四边形的对边和相等;
性质应用:①∵根据圆外切四边形的定义得:圆心到四边的距离相等.
∵平行四边形和矩形不存在一点到四边的距离相等,而菱形和正方形对角线的交点到四边的距离相等.
故答案为:B,D;
②∵圆外切四边形ABCD,∴AB+CD=AD+BC.
∵AB=12,CD=8,∴AD+BC=12+8=20,∴四边形的周长是AB+CD+AD+BC=20+20=40.
故答案为:40;
③∵相邻的三条边的比为5:4:7,∴设此三边为5x,4x,7x,根据圆外切四边形的性质得:第四边为5x+7x﹣4x=8x.
∵圆外切四边形的周长为48cm,∴4x+5x+7x+8x=24x=48,∴x=2,∴此四边形的四边为4x=8cm,5x=10cm,7x=14cm,8x=16cm.






