Question

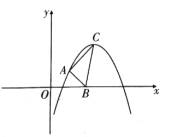
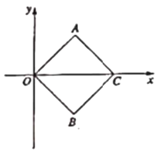
【题目】矩形OABC在直角坐标系中的位置如图所示，A，C两点的坐标分别为A(6，0)，C(0，3)，直线与BC边相交于点D．

(1)求点D的坐标；

(2)若抛物线经过D,A两点，试确定此抛物线的表达式；

(3)设（2）中抛物线的对称轴与直线OD交于点M，点P为对称轴上一动点，以P、O、M为顶点的三角形与△OCD相似，求出符合条件的P点的坐标．

Answer 1

【答案】(1)D(4,3);(2);(3)P1(3，0), P2(3,-4)

【解析】

（1）已知直线与BC交于点D（x，3），把y＝3代入等式可得点D的坐标；

（2）如图抛物线y＝ax2＋bx经过D（4，3）、A（6，0）两点，把已知坐标代入解析式得出a，b的值即可；

（3）证明Rt△P1OM∽Rt△CDO、Rt△P2MO∽Rt△DCO，根据题意再证明Rt△P2P1O≌Rt△DCO后推出CD＝P1P2＝4得出符合条件的P点坐标．

（1）由题知，直线与BC交于点D（x，3）．

把y＝3代入中得，x＝4，

∴D（4，3）；

（2）抛物线y＝ax2＋bx经过D（4，3）、A（6，0）两点，

把x＝4，y＝3；x＝6，y＝0，分别代入y＝ax2＋bx中，得

解得 ．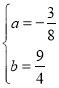

∴抛物线的解析式为；

（3）如图：抛物线的对称轴与x轴交于点P1，符合条件．

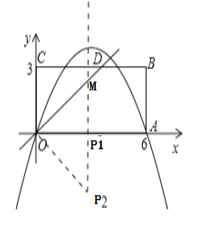
∵CB∥OA，

∴∠P1OM＝∠CDO，

∵∠DCO＝∠OP1M＝90°，

∴Rt△Q1OM∽Rt△CDO．

∵x＝＝3，

∴该点坐标为P1（3，0）．

过点O作OD的垂线交抛物线的对称轴于点P2，

∵对称轴平行于y轴，

∴∠P2MO＝∠DOC，

∴Rt△P2MO∽Rt△DCO．

在Rt△P2P1O和Rt△DCO中，

，

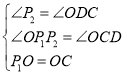∴RtP2P1O≌Rt△DCO（AAS）．

∴CD＝P1P2＝4，

∵点P2位于第四象限，

∴P2（3，4）．

因此，符合条件的点有两个，分别是P1(3，0), P2(3,-4)．