题目内容
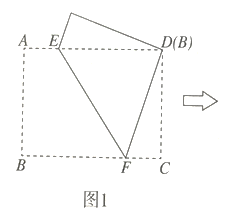
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 的坐标是
的坐标是![]() .
.
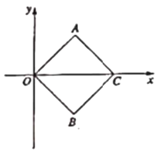
(1)正方形![]() 的边长为 ,点
的边长为 ,点![]() 的坐标是 ;
的坐标是 ;
(2)将正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() ,
,![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() ,
,![]() ,求点
,求点![]() 的坐标及旋转后的正方形与原正方形的重叠部分的面积;
的坐标及旋转后的正方形与原正方形的重叠部分的面积;
(3)动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以1个单位/秒的速度匀速运动,同时,另一动点
方向以1个单位/秒的速度匀速运动,同时,另一动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以2个单位/秒的速度匀速运动,运动时间为
方向以2个单位/秒的速度匀速运动,运动时间为![]() 秒,当它们相遇时同时停止运动,当
秒,当它们相遇时同时停止运动,当![]() 为等腰三角形时,求出
为等腰三角形时,求出![]() 的值(直接写出结果即可).
的值(直接写出结果即可).
【答案】(1)8,(![]() ,
,![]() );(2)
);(2)![]() ;(3)t=8或
;(3)t=8或![]()
【解析】
(1)由正方形性质可得AO=AC=OB=BC,AB⊥OC,OE=EC,AE=BE,由勾股定理可求AO,AE的长,即可求解;
(2)由旋转的性质可得OA=OA=4,∠OAB=∠A=90°,可求AC的长,由S重叠部分=S△OBCS△APC可求重叠部分的面积;
(3)利用分类讨论思想和等腰三角形的性质可求t的值.
解:(1)如图,连接AB,交OC于点E,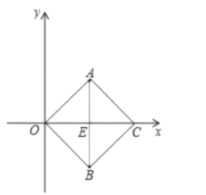
∵四边形AOBC是正方形
∴AO=AC=OB=BC,AB⊥OC,OE=EC,AE=BE,
∵点C的坐标是![]()
∴OC=![]()
∴OE=EC=![]()
∵OA2+AC2=OC2=128,
∴OA=8
∴![]()
![]()
∴正方形边长为8,点A坐标为(![]() ,
,![]() );
);
故答案为:8,(![]() ,
,![]() )
)
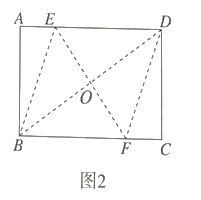
(2)如图,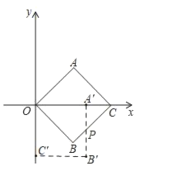
∵将正方形![]() 绕点
绕点![]() 顺时针旋转45°,∠AOC=45°
顺时针旋转45°,∠AOC=45°
∴点A落在OC上,
∴OA=OA=8,∠OAB=∠A=90°
∴点A(8,0),AC=OCOA=![]() -8
-8
∵∠ACB=45°,
∴∠APC=∠ACP=45°
∴AC=AP=![]() -8
-8
∴S重叠部分=S△OBCS△APC=![]() -
-![]() =
=![]()
(3)∵t=8时,点P与A重合,点Q与C重合,且△OAC是等腰三角形
∴当t=8时,△OPQ为等腰三角形
当点P在OA上,点Q在OB上时,OP=t,OQ=2t,则直角三角形OPQ不是等腰三角形;
当点P在OA上,点Q在BC上时,
∵△OPQ是等腰三角形
∴点Q在OP的垂直平分线上,![]()
∴![]()
∴![]()
当点P在AC上时,点Q在AC上时,OP≠OQ≠PQ
∴△OPQ不是等腰三角形.
∴当t=8或![]() 时,△OPQ为等腰三角形.
时,△OPQ为等腰三角形.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案