题目内容
【题目】如图,已知D是BC的中点,过点D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=10,AC=6,求线段CG的长.

【答案】(1)证明见解析;(2)CG=2.
【解析】
本题需先连接EC、EB,根据AE是∠CAB的平分线,得出EG=EF,再根据ED垂直平分BC,得出Rt△CGE≌Rt△BFE,从而证出BF=CG;
本题根据AE是∠CAB的平分线,得出∠FAE=∠GAE,再根据EF⊥AB于点F,EG⊥AC于点G,得出∠AFE=∠AGE ,即可证得△AFE≌△AGE ,从而得到AF=AG,
设BF=CG=x, AG=AF=y,组成二元一次方程组即可求解.
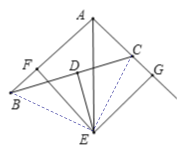
(1)连接EC、EB
![]() AE是∠CAB的平分线,
AE是∠CAB的平分线,
EF⊥AB于点F,EG⊥AC于点G,
![]() EG=EF
EG=EF
![]() 点D是BC的中点,ED垂直BC
点D是BC的中点,ED垂直BC
∴ED垂直平分BC,
![]() EC=EB
EC=EB
![]() Rt△CGE≌Rt△BFE(HL),
Rt△CGE≌Rt△BFE(HL),
![]() BF=CG
BF=CG
(2)![]() AE是∠CAB的平分线
AE是∠CAB的平分线
∴∠FAE=∠GAE
∵EF⊥AB于点F,EG⊥AC
∴∠AFE=∠AGE=90°
在△AFE和△AGE中
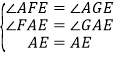 ,
,
∴△AFE≌△AGE(AAS)
∴AF=AG
设BF=CG=x, AG=AF=y
∴AB=AF+BF=x+y=10
AC=AG-CG=y-x=6
∴![]()
解得![]()
∴CG=BF=2.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目