题目内容
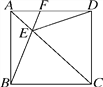
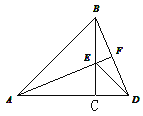
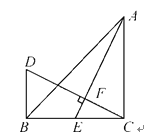
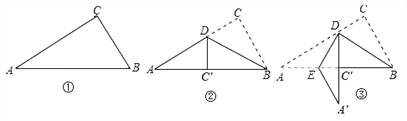
【题目】如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,若折痕DE的长是![]() cm,则BC的长是( )
cm,则BC的长是( )
A. 3cm B. 4cm C. 5cm D. 6cm
【答案】B
【解析】分析:先根据在一个直角三角形纸片,∠A=30°,根据翻折图形的性质可得:
∠DBA=30°, ∠ADC’=60°, ∠A‘DE=30°,所以∠BDE=90°,在Rt△BDE中, ∠DBE=30°,DE=![]() ,根据30°角所对直角边等于斜边的一半,可得:BE=
,根据30°角所对直角边等于斜边的一半,可得:BE=![]() ,根据勾股定理可得:BD=
,根据勾股定理可得:BD=![]() , 在Rt△DBC中, ∠DBC=30°,DB=
, 在Rt△DBC中, ∠DBC=30°,DB=![]() ,根据30°角所对直角边等于斜边的一半,可得:DC=
,根据30°角所对直角边等于斜边的一半,可得:DC=![]() ,根据勾股定理可得:BC=
,根据勾股定理可得:BC=![]() .
.
详解: 因为∠A=30°,根据翻折图形的性质可得:
∠DBA=30°, ∠ADC’=60°, ∠A‘DE=30°,
所以∠BDE=90°,
在Rt△BDE中, 因为∠DBE=30°,DE=![]() ,
,
所以BE=![]() ,
,
根据勾股定理可得:BD=![]() ,
,
在Rt△DBC中, ∠DBC=30°,DB=![]() ,根
,根
所以DC=![]() ,
,
根据勾股定理可得:BC=![]() .
.
故选B.

练习册系列答案
相关题目