题目内容
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
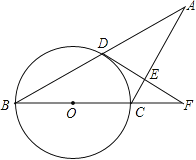
(1)求证:AD=BD;
(2)求证:DF是⊙O的切线
(3)若⊙O直径为18,![]() ,求DE的长
,求DE的长
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)连接CD,由BC为直径可知CD⊥AB,又BC=AC,由等腰三角形的底边“三线合一”证明结论;
(2)连接OD,则OD为△ABC的中位线,OD∥AC,已知DF⊥AC,可证DF⊥OC,即可证得结论;
(3)连接CD,在Rt△BCD中,已知BC=18,sinB=![]() ,求得CD=6,则AD=
,求得CD=6,则AD=![]() ,在△ACD中,利用面积法即可求出DE的长.
,在△ACD中,利用面积法即可求出DE的长.
证明:(1)连接CD
∵BC为⊙O的直径,
∴CD⊥AB.
∵AC=BC,
∴AD=BD.
(2)连接OD;
∵AD=BD,OB=OC,
∴OD是△BCA的中位线,
∴OD∥AC.
∵DE⊥AC,
∴DF⊥OD.
∵OD为半径,
∴DF是⊙O的切线
(3)在Rt△BCD中, ![]()
即![]() ,∴CD=6
,∴CD=6
在Rt△ACD中,![]()
根据直角三角形的面积可得:
![]() .
.


【题目】在![]() 中,
中,![]() ,
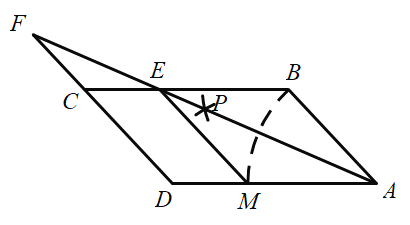
,![]() ,在图中按下列步骤进行尺规作图:
,在图中按下列步骤进行尺规作图:
① | 以 |
② | 分别以 |
③ | 画射线 |
下列说法错误的是( )
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,则
,则![]()
【题目】某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场,下表是他的技术统计.
场次 | 对阵甲队 | 对阵乙队 | ||
得分(分) | 失误(次) | 得分(分) | 失误(次) | |
第一场 | 25 | 2 | 27 | 3 |
第二场 | 30 | 0 | 31 | 1 |
第三场 | 27 | 3 | 20 | 2 |
第四场 | 26 | 2 | 26 | 4 |
(1)他在对阵甲队和乙队的各四场比赛中,平均每场得分分别是多少?
(2)利用方差判断他在对阵哪个队时得分比较稳定;
(3)根据上表提供的信息,判断他在对阵哪个队时总体发挥较好,简要说明理由.