题目内容
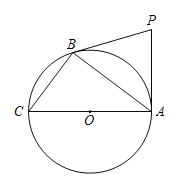
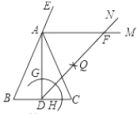
【题目】如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
A.6B.![]() C.
C.![]() D.8
D.8
【答案】D
【解析】
根据画图过程可得:DF平分∠ADC,∠ADF=∠CDF,根据AB=AC,得∠B=∠ACB,由AM是△ABC外角∠CAE的平分线,证得∠EAF=∠B,得AF∥BC,进而证明△ADF为等腰直角三角形,即可求出DF的长
解:根据画图过程可知:DF平分∠ADC,
∴∠ADF=∠CDF,
∵AB=AC,
∴∠B=∠ACB,
∵AM是△A BC外角∠CAE的平分线,
∴∠EAM=∠CAM,
∵∠EAC=∠B+∠ACB,
∴∠EAF=∠B,
∵AF//BC,
∴∠AFD=∠FDC, ∠FAD=∠ADB
∴∠AFD=∠ADF,
∴AF=AD,
∵AD是高, AB=AC=6,BC=4,
∴∠ADB=90°,![]() ,
,
∴∠FAD=∠ADB=90°
∴![]() ,
,
∵AF=AD![]() , ∠FAD=90°
, ∠FAD=90°
∴△ADF的形状是等腰直角三角形.
∴DF=![]()
故选: D.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
【题目】某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场,下表是他的技术统计.
场次 | 对阵甲队 | 对阵乙队 | ||
得分(分) | 失误(次) | 得分(分) | 失误(次) | |
第一场 | 25 | 2 | 27 | 3 |
第二场 | 30 | 0 | 31 | 1 |
第三场 | 27 | 3 | 20 | 2 |
第四场 | 26 | 2 | 26 | 4 |
(1)他在对阵甲队和乙队的各四场比赛中,平均每场得分分别是多少?
(2)利用方差判断他在对阵哪个队时得分比较稳定;
(3)根据上表提供的信息,判断他在对阵哪个队时总体发挥较好,简要说明理由.