Question

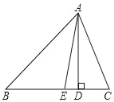
【题目】如图，在△ABC中，AD是BC边上的高，点E在BC上，AE是∠BAC的平分线，BE＝AE，∠B＝40°．

（1）求∠EAD的度数；

（2）求∠C的度数．

Answer 1

【答案】（1）10°；（2）60°．

【解析】

（1）根据等腰三角形的性质得到∠B=∠BAE=40°，根据三角形的内角和即可得到结论；
（2）根据角平分线的定义得到∠BAC=2∠BAE=80°，根据三角形的内角和即可得到结论．

解：（1）∵BE＝AE，∠B＝40°，

∴∠B＝∠BAE＝40°，

∴∠AEC＝∠BAE+∠B＝80°，

∵AD是BC边上的高，

∴∠ADE＝90°，

∴∠EAD＝180°﹣∠ADE﹣∠AEC

＝180°﹣90°﹣80°

＝10°；

（2）∵AE是∠BAC的角平分线，

∴∠BAC＝2∠BAE＝80°，

∴∠C＝180°﹣∠B﹣∠BAC，

＝180°﹣40°﹣80°

＝60°．