题目内容
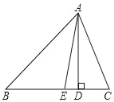
【题目】如图所示,请按照要求解答问题.
(1)数轴上的点C在2、3的正中间位置,则点C表示的数是 ,线段AB的中点D表示的数是 ;
(2)线段AB的中点D与线段BC的中点E的距离为 ;
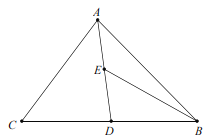
(3)在数轴上方有一点M,下方有一点N,且∠ABM=120°,∠CBN=60°,请画出示意图,并判断BC是否平分∠MBN.简要说明理由.
![]()
【答案】(1)2.5;-2;(2)2.75;(3)图详见解析,BC平分∠MBN,理由详见解析.
【解析】
(1)直接从数轴上读数即可;
(2)先求BC的中点E表示的数:(-1+2.5)÷2=0.75,再求DE的长;
(3)实际是以AB为边,在数轴上方画∠ABM=120°,下方画∠CBN=60°,根据平角的定义可求出∠MBC=60°,所以BC平分∠MBN.
解:(1)读数轴可知,C表示的数是2.5,线段AB的中点D表示的数是-2;
(2)线段BC的中点E表示的数是:(-1+2.5)÷2=0.75,
∴DE=2+0.75=2.75;
(3)示意图如图.

BC平分∠MBN.
理由:
∵∠ABM=120°,
∴∠MBC=180°-∠ABM=180°-120°=60°.
又∵∠CBN=60°,
∴∠MBC=∠CBN,即BC平分∠MBN.

练习册系列答案
相关题目