题目内容
【题目】如图,P点是灯塔所在位置,轮船A位于灯塔南偏东40°方向,轮船B位于灯塔北偏东30°方向,轮船C位于灯塔北偏西70°方向,航线PE(射线)平分∠BPC.
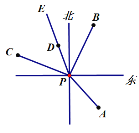
(1)求∠APE的度数;
(2)航线PE上的轮船D相对于灯塔P的方位是什么?
(以正北、正南方向为基准).
【答案】(1)160°;(2)轮船D在灯塔P北偏西20°的方位上
【解析】
(1)先求出∠BPC的度数,根据角平分线的定义,得∠BPE的度数,再求出∠APB的度数,进而即可求解;
(2)求出∠MPD的度数,进而即可求解.
(1)∵∠NPA = 40°, ∠MPB = 30°,∠MPC = 70°,
∴∠BPC = ∠MPB + ∠MPC = 30°+70°= 100°,
∵PE平分∠BPC,
∴∠BPE =![]() ∠BPC =
∠BPC =![]() ×100°=50°,
×100°=50°,
∴∠APB =180°-∠NPA-∠MPB = 180°-40°-30°=110°,
∴∠APE = ∠BPE + ∠APB = 50°+ 110°= 160° ,
(2)∵∠MPD = ∠BPE -∠MPB = 50°-30°= 20°,
∴轮船D在灯塔P北偏西20°的方位上 .

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目