题目内容
【题目】已知A、B在数轴上分别表示a、b
(1)对照数轴填写下表:
a | 6 | -6 | -6 | -6 | -10 | -2.5 |
b | 4 | 0 | 4 | -4 | 2 | -2.5 |
两点距离 | 2 | 6 | 0 |
(2)若A、B两点间的距离记为 d,试问d与a、b有何数量关系;
(3)在数轴上找到所有符合条件的整数点P,使它到5和﹣5的距离之和为10,并求出所有这些整数的和;
(4)若数轴上点C表示的数为x,当点C在什么位置时,
①|x+1|的值最小;②|x+1|+|x﹣2|的值最小.
【答案】(1)10、2、12;(2)![]() ;(3)是
;(3)是![]() 共11个点,和为0;(4)①C在-1时,有最小值;②点C在-1与2之间,有最小值
共11个点,和为0;(4)①C在-1时,有最小值;②点C在-1与2之间,有最小值
【解析】
(1)首先要明确两点间的距离,即为两数差的绝对值.
(2)明确两点间的距离,即为两数差的绝对值(d=|a-b|).
(3)由题意得|p-5|+|p-(-5)|=10,得p.
(4)解答此类问题要画出数轴,直观形象,一目了然.
解:(1)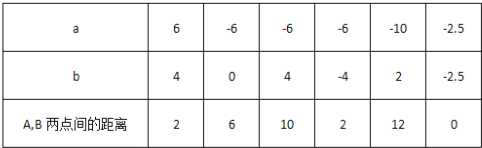
(2)d=|a-b|;
(3)由题意,得|p-5|+|p-(-5)|=10,
∴p为-5,-4,-3,-2,-1,0,1,2,3,4,5共11个点,和为0;
(4)①点C在-1;②点C在-1与2之间(包括-1和2).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目