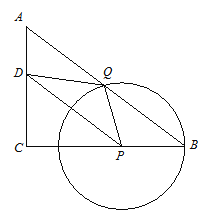
题目内容
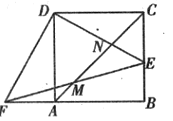
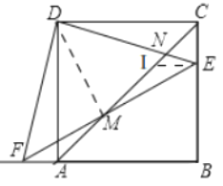
【题目】边长为4的正方形ABCD中,点E是BC边上的一个动点,连接DE,交AC于点N,过点D作DF⊥DE,交BA的延长线于点F,连接EF,交AC于点M.
(1)判定△DFE的形状,并说明理由;
(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式;并求出当x为何值时y有最大值?最大值是多少?
(3)随着点E在BC边上运动,NA·MC的值是否会发生变化?若不变,请求出NA·MC的值;若变化,请说明理由.
【答案】(1)等腰直角三角形,见解析;(2)y =﹣![]() x2+ x,当x=2,y有最大值1;(3)不变,16
x2+ x,当x=2,y有最大值1;(3)不变,16
【解析】
(1)先判断出∠FDA=∠CDE,证得△ADF≌△CDE,即可得出结论;
(2)利用平行线分线段成比例定理得出比例式表示出AF边上的高,即可得出结论;
(3)先判断出△FAM≌△EIM,得出ME=FM,再判断出△AND∽△CDM,即可得出结论.
(1)在正方形ABCD中,AD=CD,∠ADC=∠DCB=∠DAB =90°,
∵∠FDE=∠ADC=90°,
∴∠FDA=∠CDE,
在△ADF和△CDE中,
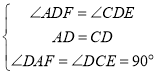 ,
,
∴△ADF≌△CDE,
∴DE =DF,
∴△DFE为等腰直角三角形;
(2)过M作MG⊥AB于G,
设MG=h,
又∵∠GAM =45°,
∴AG =MG=h,由(1)知FA=CE =![]() ,
,
∵CB⊥AB,
∴MG//BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴h=![]() ,
,
∴y =![]()
![]() ·
·![]() =
=![]()
![]()
![]()
![]() (
(![]() );
);
![]() ,
,
∵![]() ,
,
∴当![]() ,
,![]() 有最大值1;
有最大值1;
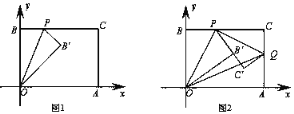
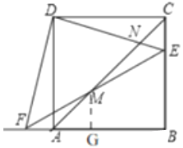
(3)不变,如图3,过点E作EI∥AB交AC于I,连接DM,
∴∠EIC=∠ICE=45°,
∴EI=EC=AF,
∵EI∥AB,
∴∠FAM=∠MIE,∠MFA=∠IEM,
∴△FAM≌△EIM,
∴ME=FM,
由(1)可得,△FDE是等腰直角三角形,
∴DM⊥EF,
∴∠MDE=45°,∠MDC=45°+∠CDN=∠DNA,
∵∠DAN=∠DCM=45°,
∴△AND∽△CDM,
∴![]() ,
,
∴ANCM=ADCD=16.