Question

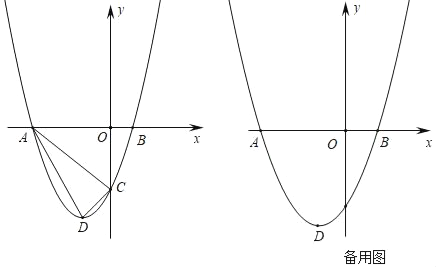
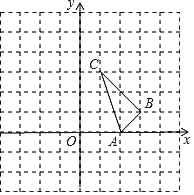
【题目】如图，在平面直角坐标系中，已知A（2，0）、B（3，1）、C（1，3）．

（1）将△ABC沿x轴负方向移动2个单位长度至△A1B1C1，画图并写出点C1的坐标；

（2）以点A1为旋转中心，将△A1B1C1逆时针方向旋转90°得到△A2B2C2，画图并写出点C2的坐标；

（3）以B、C1、C2为顶点的三角形是　 　三角形，其外接圆的半径R＝　 　．

Answer 1

【答案】（1）C1的坐标为（﹣1，3）;（2）（﹣3，﹣1）；（3）直角,．

【解析】

（1）将三个顶点分别向左平移2个单位得到其对应点，再顺次连接即可得；

（2）将三个顶点分别以点A1为旋转中心，逆时针方向旋转90°得到对应点，再顺次连接即可得；

（3）利用勾股定理及其逆定理（如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形）求解可得．

解：（1）如图所示，△A1B1C1即为所求，其中C1的坐标为（﹣1，3）．

（2）如图所示，△A2B2C2即为所求，其中点C2的坐标为（﹣3，﹣1）；

（3）∵C1C22＝BC12＝22+42＝20，BC22＝22+62＝40，

∴C1C22+BC12＝BC22，

∴△BC1C2是直角三角形，

则外接圆的半径R＝BC2＝×2＝．

故答案为：直角，．