题目内容
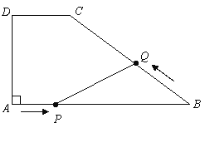
【题目】如图,在梯形ABCD中,DC//AB,∠A=90°,AD=6cm,DC=4cm,BC的坡度i=3:4,动点P从A出发以2cm/s的速度沿AB方向向点B运动,动点Q从点B出发以3厘cm/s的速度沿B→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
(1)求边BC的长;
(2)当t为何值时,PC与BQ相互平分;
(3)连结PQ,设△PBQ的面积为y,探求y与t的函数关系式,求t为何值时,y有最大值?最大值是多少?
【答案】(1)BC=10;(2)![]() 秒时;PC与BQ相互平分;(3)
秒时;PC与BQ相互平分;(3)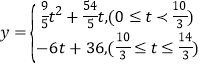 ,当
,当![]() 时,
时,![]() 有最大值,为
有最大值,为![]() 厘米2.
厘米2.
【解析】
(1)作CE⊥AB于E,根据坡度的定义进行求解;
(2)要使PC与BQ相互平分,只需保证四边形CPBQ是平行四边形,即可得到关于t的方程,进行求解;
(3)此题要分两种情况考虑:点Q在BC上,即![]() 时;当点Q在CD上,即
时;当点Q在CD上,即![]() 根据三角形的面积公式建立函数关系式,再进一步求解.
根据三角形的面积公式建立函数关系式,再进一步求解.
解:(1)作CE⊥AB于E,则四边形ADCE是矩形,
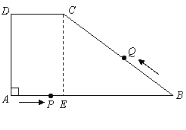
则CE=AD=6.
又BC的坡度i=CE:BE=3:4,且BE⊥CE,
则CE:BC=3:5,
则BC=10;
(2)要使PC与BQ相互平分,只需保证四边形CPBQ是平行四边形,即PB=CQ.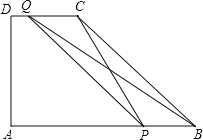
由(1),得AB=4+8=12,则PB=122t.
则122t=3t10,
t=4.4.
(3)当![]() 时,则BP=122t,
时,则BP=122t,![]()
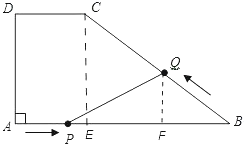
![]()
当t=3时,y最大,是16.2;
当![]() 时,则
时,则![]()
则t=![]() 时,y取得最大值,是16.
时,y取得最大值,是16.
综上所述,则当t=3时,y取得最大值,是16.2.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目