题目内容
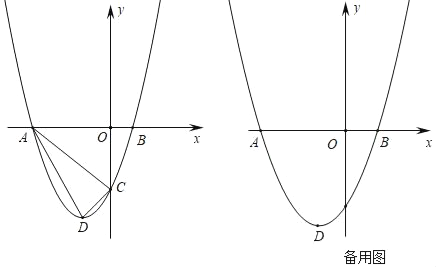
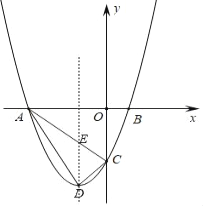
【题目】如图,抛物线y=ax2+2ax﹣3a(a>0)交x轴于A、B两点,交y轴于点C,抛物线的顶点为D.
(1)填空:抛物线的对称轴为 ,点A的坐标为 ;点B的坐标为 ;
(2)若△ADC的面积为3,求抛物线的解析式;
(3)在(2)的条件下,当m≤x≤m+1,y的取值范围是﹣4≤y≤2m,求m的值.
【答案】(1)x=﹣1,(﹣3,0),(1,0);(2)y=x2+2x﹣3;(3)m的值为:﹣2或﹣![]() 或﹣1或0.
或﹣1或0.
【解析】
(1)令y=0,则x=﹣3或1,令x=0,则y=﹣3a,即可求解;
(2)利用S△ADC=![]() ED×OA=
ED×OA=![]() ×2a×3=3,即可求解;
×2a×3=3,即可求解;
(3)分①m+1≤﹣1②m+1>﹣1且m<﹣1③m≥﹣1,三种情况分别求解即可.
解:(1)令y=0,则x=﹣3或1,令x=0,则y=﹣3a,
故点A、B、C的坐标分别为(﹣3,0)、(1,0)、(0,﹣3a),
函数对称轴为x=﹣1,点D的坐标为(﹣1,﹣4a),
故:答案为:x=﹣1,(﹣3,0),(1,0);
(2)过点D作函数对称轴交直线AC于点E,
点A、C的坐标分别为(﹣3,0)、(0,﹣3a),则直线AC的表达式为:y=kx﹣3a,
将点A坐标代入上式并解得:k=﹣ax﹣3a,点E(﹣1,﹣2a),
S△ADC=![]() ED×OA=
ED×OA=![]() ×2a×3=3,解得:a=1,
×2a×3=3,解得:a=1,
故抛物线表达式为:y=x2+2x﹣3;
(3)①当m+1≤﹣1时,即:m≤﹣2,
函数在x=m+1处取得最小值,即:(m+1)2+2(m+1)﹣3=﹣4,解得:m=﹣2,
函数在x=m处取得最大值,m2+2m﹣3=2m,解得:m=![]() (舍去),
(舍去),
故:m=﹣2;
②当m+1>﹣1,且m<﹣1,即:﹣2<m<﹣1时,
同理可得:m=![]() ;
;
③当m≥﹣1时,
同理可得:m=﹣1或0;
故:m的值为:﹣2或﹣![]() 或﹣1或0.
或﹣1或0.

【题目】如图,已知![]() 是
是![]() (
(![]() )的函数,表1中给出了几组
)的函数,表1中给出了几组![]() 与
与![]() 的对应值:
的对应值:
表1:
| … |
| 1 |
| 2 |
| 3 | … |
| … | 6 | 3 | 2 |
|
| 1 | … |

(1)以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
(2)如果一次函数图像与(1)中图像交于![]() 和
和![]() 两点,在第一、四象限内当
两点,在第一、四象限内当![]() 在什么范围时,一次函数的值小于(1)中函数的值?请直接写出答案.
在什么范围时,一次函数的值小于(1)中函数的值?请直接写出答案.