Question

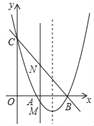
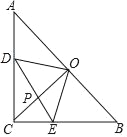
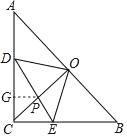
【题目】在Rr△ABC中，∠C＝90°，AC＝BC＝1，点O为AB的中点，点D、E分别为AC、AB边上的动点，且保持DO⊥EO，连接CO、DE交于点P．

（1）求证：OD＝OE；

（2）在运动的过程中，DPEP是否存在最大值？若存在，请求出DPEP的最大值；若不存在，请说明理由．

（3）若CD＝2CE，求DP的长度．

Answer 1

【答案】（1）证明见解析（2）DPEP存在最大值为（3）PG＝，PD＝

【解析】

（1）证明△ADO≌△CEO，可得OD＝OE；

（2）先根据对角互补证明D、C、E、O四点共圆，再得△DPO∽△CPE，列比例式可得：PDEP＝CPPO，设CP＝x，则OP＝﹣x，则CPPO＝x（﹣x ）＝﹣，根据二次函数的最值问题得出DPEP存在最大值为；

（3）设CE＝a，则CD＝2a，根据AC＝1列等式求出，a＝，则CE＝，CD＝，根据勾股定理求DE的长，作辅助线构建平行线，得相似，列比例式可求得DP的长．

证明：（1）∵AC＝BC＝1，点O为AB的中点，

∴CO⊥AB，CO＝AO，

∴∠COA＝90°，

∴∠DOP+∠AOD＝90°，

∵DO⊥OE，

∴∠DOP+∠POE＝90°，

∴∠AOD＝∠POE，

同理∠A＝∠OCE，

∴△ADO≌△CEO，

∴OD＝OE；

（2）∵∠ACB＝90°，∠DOE＝90°，

∴∠ACB+∠DOE＝180°，

∴D、C、E、O四点共圆，

∴∠ODP＝∠PCE，∠DPO＝∠CPE，

∴△DPO∽△CPE，

∴，

∴PDEP＝CPPO，

在Rt△ACB中，AB＝，

∴CO＝AO＝BO＝，

设CP＝x，则OP＝﹣x，

则CPPO＝x（﹣x ）＝﹣＝﹣（x﹣）2+，

即当x＝时，CPPO有最大值为，

也就是DPEP存在最大值为；

（3）设CE＝a，则CD＝2a，

由（1）得：AD＝CE＝a，

∵AC＝1，

∴a+2a＝1，

a＝，

∴CE＝，CD＝，

由勾股定理得：DE＝，

过P作PG∥BC，交AC于G，

∵∠DCO＝45°，

∴PG＝CG，

∵PG∥CE，

∴△DGP∽△DCE，

∴，

∴，

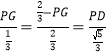∴PG＝，PD＝．