题目内容
 如图,在菱形ABCD中,DE⊥AB,垂足为E,
如图,在菱形ABCD中,DE⊥AB,垂足为E, ,BE=1,F是BC的中点.现有下列四个结论:①DE=3;②四边形DEBC的面积等于9;③(AC+BD)(AC-BD)=80;④DF=DE.其中正确结论的个数为
,BE=1,F是BC的中点.现有下列四个结论:①DE=3;②四边形DEBC的面积等于9;③(AC+BD)(AC-BD)=80;④DF=DE.其中正确结论的个数为
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:可设DE=3k,则AE=4k,AD=5K,BE=k,从而求出边长及高,计算面积;连接BD、AC,根据勾股定理可求对角线的长度;
作DH⊥BC于H点,则DH=DE,比较DH与DF的大小.
解答: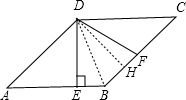 解:设DE=3k,则AE=4k,AD=5K,BE=k=1,
解:设DE=3k,则AE=4k,AD=5K,BE=k=1,
∴AB=5,DE=3.故①正确;
S梯形DEBC= ×(1+5)×3=9,故②正确;
×(1+5)×3=9,故②正确;
∵DE=3,EB=1,∴DB= .
.
又∵SABCD=AB×DE=5×3=15,
SABCD= ×BD×AC,
×BD×AC,
∴15= ×
× ×AC,
×AC,
AC=3 .
.
(AC+BD)(AC-BD)
=AC2-BD2=(3 )2-
)2- 2=90-10=80.故③正确;
2=90-10=80.故③正确;
作DH⊥BC于H点.
∵DE⊥AB,DH⊥BC,∠ABD=∠CBD,
∴DE=DH.
又DH<DF,
∴DE<DF.故④错误.
所以①②③正确.
故选C.
点评:此题主要考查了菱形的性质及面积计算,有一定的综合性,属中等难度.
分析:可设DE=3k,则AE=4k,AD=5K,BE=k,从而求出边长及高,计算面积;连接BD、AC,根据勾股定理可求对角线的长度;
作DH⊥BC于H点,则DH=DE,比较DH与DF的大小.
解答:
 解:设DE=3k,则AE=4k,AD=5K,BE=k=1,
解:设DE=3k,则AE=4k,AD=5K,BE=k=1,∴AB=5,DE=3.故①正确;
S梯形DEBC=
 ×(1+5)×3=9,故②正确;
×(1+5)×3=9,故②正确;∵DE=3,EB=1,∴DB=
 .
.又∵SABCD=AB×DE=5×3=15,
SABCD=
 ×BD×AC,
×BD×AC,∴15=
 ×
× ×AC,
×AC,AC=3
 .
.(AC+BD)(AC-BD)
=AC2-BD2=(3
 )2-
)2- 2=90-10=80.故③正确;
2=90-10=80.故③正确;作DH⊥BC于H点.
∵DE⊥AB,DH⊥BC,∠ABD=∠CBD,
∴DE=DH.
又DH<DF,
∴DE<DF.故④错误.
所以①②③正确.
故选C.
点评:此题主要考查了菱形的性质及面积计算,有一定的综合性,属中等难度.

练习册系列答案
相关题目
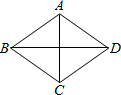 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.