��Ŀ����
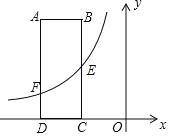
����Ŀ����ͼ����ֱ������ϵxOy�У�����ABCD��DC����x���ϣ�D������Ϊ����6��0����AB��AD�ij��ֱ�Ϊ3��8��E��BC���е㣬����������y��![]() ��ͼ����E����AD�߽��ڵ�F��
��ͼ����E����AD�߽��ڵ�F��
��1����k��ֵ������A��E�����һ�κ����ı���ʽ��
��2����x������һ��P��ʹPE+PF��ֵ��С���������P�����ꣻ
��3���ڣ�2���������£�����EF��PE��PF����ֱ��AE����һ��Q��ʹ��S��QEF��S��PEFֱ��д������������Q�����꣮
���𰸡���1��k����12��y����![]() x����2��P����5��0������3��Q����
x����2��P����5��0������3��Q����![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��������
��1����ȷ����B��C���꣬�����ó���E���꣬����ô���ϵ�����������ֱ��AE����ʽ��
��2�����ҳ���F����x��ĶԳƵ�F�������꣬�������ֱ��EF���Ľ���ʽ����һ�����ɵó����ۣ�
��3���������PEF������������ֱ��EF�Ľ���ʽ�������Q�����꣬��������ϵ��������������ķ�������������⣬�����ó����ۣ�
�⣺��1���ھ���ABCD�У�AB��3��AD��8��
��CD��AB��3��BC��AD��8��
��D����6��0����
��A����6��8����C����3��0����B����3��8����
��E��BC���е㣬
��E����3��4����
�ߵ�E�ڷ���������y��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��k����3��4����12��
�辭��A��E�����һ�κ����ı���ʽΪy��k��x+b��
��![]() �����
����� ��
��
�ྭ��A��E�����һ�κ����ı���ʽΪy����![]() x��
x��
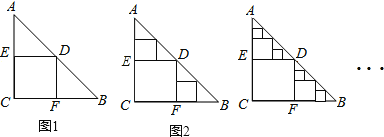
��2����ͼ1���ɣ�1��֪��k����12��
�෴���������Ľ���ʽΪy����![]() ��
��
�ߵ�F�ĺ�����Ϊ��6�����F��������Ϊ2����F����6��2����
����F����x��ĶԳƵ�F������F������6����2����
����EF����x���ڵ�P����ʱ��PE+PF��ֵ��С��
��E����3��4����
��ֱ��EF���Ľ���ʽΪy��2x+10��
��y��0����2x+10��0�����x����5��
��P����5��0����

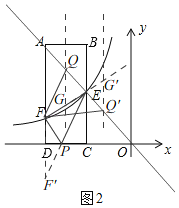
��3����ͼ2���ɣ�2��֪��F������6����2����
��E����3��4����F����6��2����
��S��PEF��S��EFF����S��PFF����![]() ����2+2��������3+6����
����2+2��������3+6����![]() ��2+2��������5+6����4��
��2+2��������5+6����4��
��E����3��4����F����6��2����
��ֱ��EF�Ľ���ʽΪy��![]() x+6��
x+6��
�ɣ�1��֪������A��E�����һ�κ����ı���ʽΪy����![]() x��
x��
���Q��m����![]() m����
m����
����Q��y���ƽ���߽�EF��G��
��G��m��![]() m+6����
m+6����
��QG��|��![]() m��
m��![]() m��6|��|2m+6|��
m��6|��|2m+6|��
��S��QEF��S��PEF��
��S��QEF��![]() |2m+6|������3+6����4��
|2m+6|������3+6����4��
��m����![]() ��m����
��m����![]() ��
��
��Q����![]() ��
��![]() ����
����![]() ��
��![]() ����
����

 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�