ƒøƒ⁄»ð
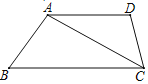
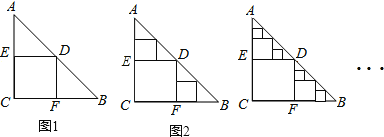
°æƒø°ø°˜ABC «“ª’≈µ»—¸÷±Ω«»˝Ω«–Œ÷Ω∞£¨°œC=Rt°œ£¨AC=BC=2£¨‘⁄’‚’≈÷Ω∞Â÷–ºÙ≥ˆ“ª∏ˆæ°ø…ƒÐ¥Ûµƒ’˝∑Ω–Œ≥∆Œ™µ⁄1¥ŒºÙ»°£¨º«À˘µ√’˝∑Ω–Œ√ʪ˝Œ™s1£®»ÁÕº1£©£ª‘⁄”ýœ¬µƒRt°˜ADE∫ÕRt°˜BDF÷–£¨∑÷±ºÙ»°’˝∑Ω–Œ£¨µ√µΩ¡Ω∏ˆœýÕ¨µƒ’˝∑Ω–Œ£¨≥∆Œ™µ⁄2¥ŒºÙ»°£¨≤¢º«’‚¡Ω∏ˆ’˝∑Ω–Œ√ʪ˝∫ÕŒ™s2£®»ÁÕº2£©£ªºÃ–¯≤Ÿ◊˜œ¬»•°≠£ª‘Úµ⁄10¥ŒºÙ»° ±£¨s10= £ªµ⁄2012¥ŒºÙ»°∫Û£¨”ýœ¬µƒÀ˘”––°»˝Ω«–Œµƒ√ʪ˝÷Æ∫Õ «
°æ¥∞∏°ø![]() £ª
£ª![]() £Æ
£Æ
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫∏˘æð“‚£¨ø…«Ûµ√S°˜AED+S°˜DBF=S’˝∑Ω–ŒECFD=S1=1£¨Õ¨¿Ìø…µ√πʬ…£∫Snº¥ «µ⁄n¥ŒºÙ»°∫Û £”ý»˝Ω«–Œ√ʪ˝∫Õ£¨∏˘æð¥Àπʬ…«ÛΩ‚º¥ø…¥∞∏£Æ
‘Ã‚Ω‚Œˆ£∫°þÀƒ±þ–ŒECFD «’˝∑Ω–Œ£¨
°ýDE=EC=CF=DF£¨°œAED=°œDFB=90°„£¨
°þ°˜ABC «µ»—¸÷±Ω«»˝Ω«–Œ£¨
°ý°œA=°œC=45°„£¨
°ýAE=DE=EC=DF=BF=EC=CF£¨
°þAC=BC=2£¨
°ýDE=DF=1£¨
°ýS°˜AED+S°˜DBF=S’˝∑Ω–ŒECFD=S1=1£ª
Õ¨¿Ì£∫S2º¥ «µ⁄∂˛¥ŒºÙ»°∫Û £”ý»˝Ω«–Œ√ʪ˝∫Õ£¨
Snº¥ «µ⁄n¥ŒºÙ»°∫Û £”ý»˝Ω«–Œ√ʪ˝∫Õ£¨
°ýµ⁄“ª¥ŒºÙ»°∫Û £”ý»˝Ω«–Œ√ʪ˝∫ÕŒ™£∫2©ÅS1=1=S1£¨
µ⁄∂˛¥ŒºÙ»°∫Û £”ý»˝Ω«–Œ√ʪ˝∫ÕŒ™£∫S1©ÅS2=1©Å![]() =
=![]() =S2£¨
=S2£¨
µ⁄»˝¥ŒºÙ»°∫Û £”ý»˝Ω«–Œ√ʪ˝∫ÕŒ™£∫S2©ÅS3=![]() ©Å
©Å![]() =
=![]() =S3£¨
=S3£¨
°≠
µ⁄n¥ŒºÙ»°∫Û £”ý»˝Ω«–Œ√ʪ˝∫ÕŒ™£∫Sn©Å1©ÅSn=Sn=![]() £Æ
£Æ
‘Ús10=![]() =
=![]() £ªs2012=
£ªs2012=![]() =
=![]() £Æ
£Æ

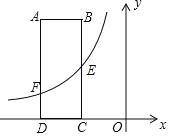
°æƒø°ø“—÷™![]() «
«![]() µƒ∫Ø ˝£¨◊‘±‰¡ø
µƒ∫Ø ˝£¨◊‘±‰¡ø![]() µƒ»°÷µ∑∂ŒßŒ™
µƒ»°÷µ∑∂ŒßŒ™![]() £¨œ¬±Ì «
£¨œ¬±Ì «![]() ”Î
”Î![]() µƒº∏◊È∂‘”¶÷µ
µƒº∏◊È∂‘”¶÷µ
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | °≠ |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | °≠ |
–°√˜∏˘æð—ßœ∞∫Ø ˝µƒæ≠—È£¨¿˚”√…œ ˆ±Ì∏ÒÀ˘∑¥”≥≥ˆµƒ![]() ”Î
”Î![]() ÷ƺ‰µƒ±‰ªØπʬ…£¨∂‘∏√∫Ø ˝µƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø.œ¬√Ê «–°√˜µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£∫
÷ƺ‰µƒ±‰ªØπʬ…£¨∂‘∏√∫Ø ˝µƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø.œ¬√Ê «–°√˜µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£∫
(1)»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷∏≥ˆ¡À“‘…œ±Ì÷–∏˜∂‘∂‘”¶÷µŒ™◊¯±Íµƒµ„. ∏˘æð√Ë≥ˆµƒµ„£¨ª≠≥ˆ∏√∫Ø ˝µƒÕºœÛ.

(2)∏˘æðª≠≥ˆµƒ∫Ø ˝ÕºœÛÃÓø’.
¢Ÿ∏√∫Ø ˝ÕºœÛ”Î![]() ÷·µƒΩªµ„◊¯±ÍŒ™_____.
÷·µƒΩªµ„◊¯±ÍŒ™_____.
¢⁄÷±Ω”–¥≥ˆ∏√∫Ø ˝µƒ“ªÃı–‘÷ .
°æƒø°øƒ≥–°«¯Œ™¡À¥ŸΩ¯…˙ªÓ¿¨ª¯µƒ∑÷¿ý¥¶¿Ì£¨Ω´…˙ªÓ¿¨ª¯∑÷Œ™£∫ø…ªÿ¿¨ª¯°¢≥¯”ý¿¨ª¯°¢∆‰À˚¿¨ª¯»˝¿ý£¨∑÷±º«Œ™A£¨B£¨C£∫≤¢«“…Ë÷√¡Àœý”¶µƒ¿¨ª¯œ‰£¨“¿¥Œº«Œ™a£¨b£¨c£Æ
£®1£©»ÙΩ´»˝¿ý¿¨ª¯Àʪ˙Õ∂»Î»˝∏ˆ¿¨ª¯œ‰£¨«Îƒ„”√ ˜–ŒÕºµƒ∑Ω∑®«Û¿¨ª¯Õ∂∑≈’˝»∑µƒ∏≈¬ £∫
£®2£©Œ™¡Àµ˜≤È–°«¯¿¨ª¯∑÷¿ýÕ∂∑≈«Èøˆ£¨œ÷Àʪ˙≥È»°¡À∏√–°«¯»˝¿ý¿¨ª¯œ‰÷–◊Ð÷ÿ500kg…˙ªÓ¿¨ª¯£¨ ˝æð»Áœ¬£®µ•Œª£∫£©
a | b | c | |
A | 40 | 15 | 10 |
B | 60 | 250 | 40 |
C | 15 | 15 | 55 |
‘π¿º∆°∞≥¯”ý¿¨ª¯°±Õ∂∑≈’˝»∑µƒ∏≈¬ £Æ