题目内容
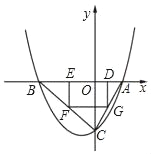
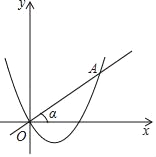
【题目】如图，已知二次函数y=ax2+bx的图象与正比例函数y=kx的图象相交于点A（3，2），有下面四个结论：①ab＞0；②a﹣b＞﹣
；③sinα=
；④不等式kx≤ax2+bx的解集是0≤x≤3．其中正确的是（ ）
A. ①② B. ②③ C. ①④ D. ③④
【答案】B
【解析】
根据抛物线图象性质确定a、b符号，把点A代入y=ax2+bx得到a与b数量关系，代入②，不等式kx≤ax2+bx的解集可以转化为函数图象的高低关系．
解：根据图象抛物线开口向上，对称轴在y轴右侧，则a＞0，b＜0，则①错误
将A（3，2）代入y=ax2+bx，则2=9a+3b
∴b=
，
∴a﹣b=a﹣（）=4a﹣
＞-，故②正确；
由正弦定义sinα=
，则③正确；
不等式kx≤ax2+bx从函数图象上可视为抛物线图象不低于直线y=kx的图象
则满足条件x范围为x≥3或x≤0，则④错误．
故答案为：B．
练习册系列答案
相关题目
【题目】某中学举行“中国梦·校园好声音”歌手大赛，高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩（满分100）如下图所示：
根据图示信息，整理分析数据如下表：
平均数（分） | 中位数（分） | 众数（分） | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
（说明：图中虚线部分的间隔距离均相等）
（1）求出表格中
的值；
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．