题目内容
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
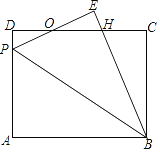
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH.
(2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程.
试题解析:
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=![]() ,
,
∴DP=![]() .
.
【题型】解答题
【结束】
25
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
【答案】(1)A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元;(2)最少购进A品牌工具套装17套.
【解析】试题分析:(1)利用两种套装的套数作为等量关系列方程求解.(2)利用总获利大于等于120,解不等式.
试题解析:
(1)解:设B种品牌套装每套进价为x元,则A种品牌套装每套进价为(x+2.5)元.
根据题意得: ![]() =2×
=2×![]() ,
,
解得:x=7.5,
经检验,x=7.5为分式方程的解,
∴x+2.5=10.
答:A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元.
(2)解:设购进A品牌工具套装a套,则购进B品牌工具套装(2a+4)套,
根据题意得:(13﹣10)a+(9.5﹣7.5)(2a+4)>120,
解得:a>16,
∵a为正整数,
∴a取最小值17.
答:最少购进A品牌工具套装17套.