题目内容
【题目】当![]() 时,
时,![]() ,则
,则![]() 的取值范围是_______.
的取值范围是_______.
【答案】m≥1
【解析】
设函数![]() ,令y=0,求出x,根据函数图像可知:在
,令y=0,求出x,根据函数图像可知:在![]() 或
或![]() 时,函数图像在-3≤x≤0的区域内位于x轴下方,再分
时,函数图像在-3≤x≤0的区域内位于x轴下方,再分![]() 或
或![]() 两种情况分别求解,最后合并.
两种情况分别求解,最后合并.
解:设函数![]() ,
,
则该函数的图像为开口向下的抛物线,
令:![]() ,得:
,得:
![]() =
=![]() =
=![]() ,
,
![]() =
=![]() =
=![]() ,
,
可得![]() ,
,
∴函数![]() 与x轴的交点为:
与x轴的交点为:
(![]() ,0),(
,0),(![]() ,0),
,0),
由于-3≤x≤0时,
![]() ,即函数
,即函数![]() 的图像在-3≤x≤0时位于x轴下方,根据函数图像可知:在
的图像在-3≤x≤0时位于x轴下方,根据函数图像可知:在![]() 或
或![]() 时,函数图像在-3≤x≤0的区域内位于x轴下方,
时,函数图像在-3≤x≤0的区域内位于x轴下方,
因此有![]() 或
或![]() 两种情况,
两种情况,
当![]() 时,函数
时,函数![]() 的对称轴直线x=m大于
的对称轴直线x=m大于![]() ,即m>0,
,即m>0,
![]() ≥0,
≥0,
![]() ,
,
∵m>0,
∴![]() ,得:m≥1,
,得:m≥1,
当![]() 时,函数
时,函数![]() 的对称轴直线x=m小于
的对称轴直线x=m小于![]() ,即m<-3,
,即m<-3,
![]() ,
,
![]() ,
,
∵m<-3,
∴m+3<0,
∴-(m+3)≥![]() ,
,
两边平方得:![]() ,
,
∵m<-3,
∴不成立,
故m的取值范围是m≥1.
故答案为:m≥1.

 名校课堂系列答案
名校课堂系列答案【题目】为全面贯彻党的教育方针和落实阳光体育运动,提高青少年学生身体健康水平和体育运动水平,某校准备购买一批篮球,甲、乙两家商店的标价都是每个![]() 元,两家商店推出不同的优惠方式如下表:
元,两家商店推出不同的优惠方式如下表:
商店 | 优惠方式 |
甲 | 购买数量不超过 |
乙 | 按照标价的八折销售 |
(1)设该学校购买![]() 个篮球,在甲商店购买花费
个篮球,在甲商店购买花费![]() 元,在商店购买花费
元,在商店购买花费![]() 元,请分别求出
元,请分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若学校需购买![]() 个篮球,请你通过计算进行对比,选择哪家商店更省钱?
个篮球,请你通过计算进行对比,选择哪家商店更省钱?
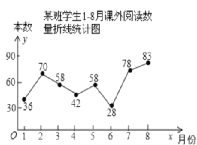
【题目】甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷):
品种 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
甲 |
|
|
| 10 |
|
乙 |
|
|
|
|
|
(1)乙种水稻5年的平均单位面积产量的平均数为______吨/公顷;
(2)“扇形统计图”和“折线统计图”中,更能直观地反映甲种水稻5年的平均单位面积产量变化过程和趋势的统计图是______;
(3)王老汉家有100公顷田要种植水稻,你建议他种什么品种的水稻,并说明理由.