题目内容
【题目】已知一次函数y=kx+b(k≠0)的图象经过A(3,18)和B(﹣2,8)两点.
(1)求一次函数的解析式;
(2)若一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象只有一个交点,求交点坐标.
(m≠0)的图象只有一个交点,求交点坐标.
【答案】(1)一次函数的解析式为y=2x+12;(2)(﹣3,6).
【解析】
(1)直接把(3,18),(﹣2,8)代入一次函数y=kx+b中可得关于k、b的方程组,再解方程组可得k、b的值,进而求出一次函数的解析式;
(2)联立一次函数解析式和反比例函数解析式可得2x2+12x﹣m=0,再根据题意得到△=0时,两函数图像只有一个交点,解方程即可得到结论.
解:(1)把(3,18),(﹣2,8)代入一次函数y=kx+b(k≠0),得
![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=2x+12;
(2)∵一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象只有一个交点,
(m≠0)的图象只有一个交点,
∴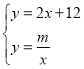 只有一组解,
只有一组解,
即2x2+12x﹣m=0有两个相等的实数根,
∴△=122﹣4×2×(﹣m)=0,
∴m=-18.
把m=-18代入求得该方程的解为:x=-3,
把x=-3代入y=2x+12得:y=6,
即所求的交点坐标为(-3,6).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目