题目内容
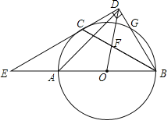
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() 的外角平分线
的外角平分线![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 的延长线于
的延长线于![]() .
.
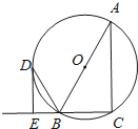
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,由OB=OD,得出∠ODB=∠OBD,根据BD是△ABC的外角平分线,推出∠ODB=∠DBE,得到OD∥BE.推出BE⊥DE,根据AB是⊙O的直径,得到AC⊥CE,根据DE∥AC,即可推出OD⊥DE,从而证得直线DE与⊙O相切.
(2)由∠A=30°,根据三角形的外角性质求出∠DBE,进而求出∠DOB=60°,即可得出结论.
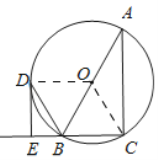
解:(1)如图,连接![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的外角平分线,
的外角平分线,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 且点
且点![]() 在
在![]() 上.
上.
∴直线![]() 与
与![]() 相切;
相切;
(2)如图,连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?